Let f(x, y) = xy(x2 − y2) / (x2 y2) with f(0, 0) = 0 The question was asking to proof f(x, y) continuous everywhere One way to solve it was to just change x = rcos(θ), y = rsin(θ) and solved
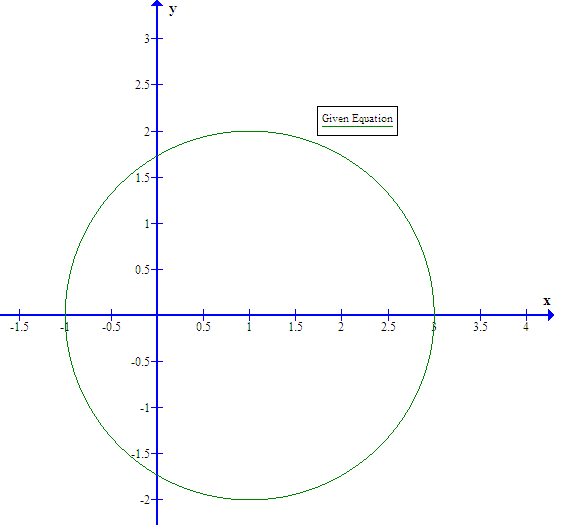
X^2+y^2=1 graph-Tìm các giá trị của tham số m để đồ thị hàm số y = 2x 3 3( m3) x 2 11 3m có hai điểm cực trị Đồng thời hai điểm cực trị đó và điểm C( 0;Daerah penyelesaian dari sistem pertidaksamaan y lebih dari x kuadrat 2x1, x2y lebih dari sama dengan 2, ditunjukkan oleh grafik
X^2+y^2=1 graphのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 |  |  |
 | ||
「X^2+y^2=1 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 |  | |
「X^2+y^2=1 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
 |  |  |
「X^2+y^2=1 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 | ||
 |  |  |
「X^2+y^2=1 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 | ||
「X^2+y^2=1 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 |  |  |
「X^2+y^2=1 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
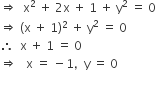 |  | |
 |  |  |
 |  |  |
 |  | |
「X^2+y^2=1 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
「X^2+y^2=1 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |
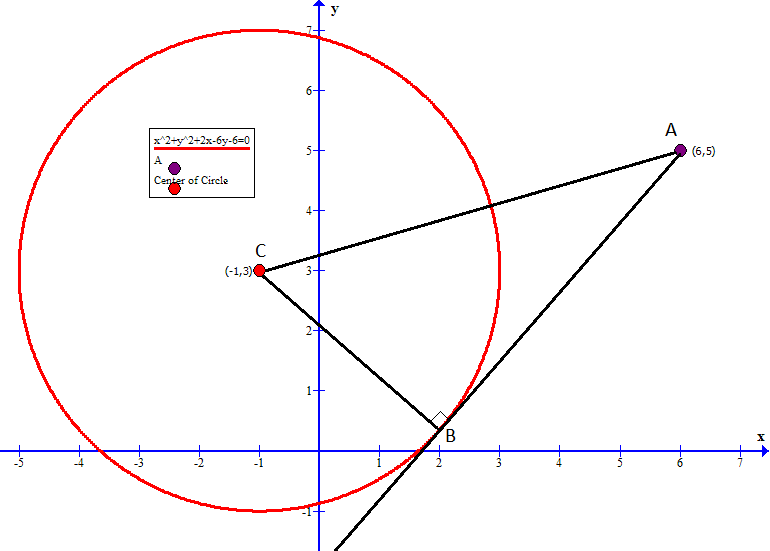
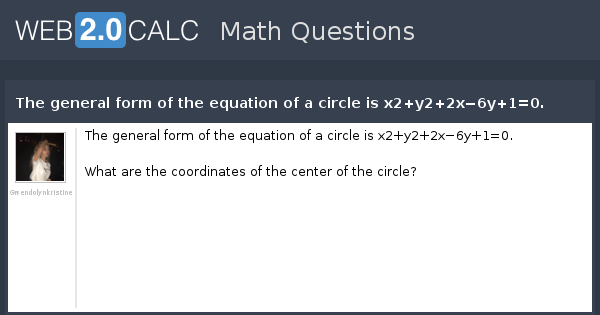
Free PreAlgebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators stepbystepFrom the equation of line it is clear that line passes through origin Also the circle touches the origin So point A is (0,0) now put x=y in equation of circle After solving for this you will get x2 y2 −
Incoming Term: x^2-y^2+2x+1, x^2+y^2=1, x^2+y^2=1 graph, x^2+y^2=1 derivative, (x^2+y^2-1)^3, x^2+y^2=1/4, x^2+y^2=1 dy/dx, x^2+y^2=1-z, x^2+y^2+xy=1, x ^ 2 + (y - 3 sqrt(2x)) ^ 2 = 1,




0 件のコメント:
コメントを投稿