Use A = int_a^b(y_1(x)y_2(x))dx where y_1(x) >= y_2(x) Find the x coordinates of endpoints of the area 6x x^2 = x^2 2x 0 = 2x^28x x = 0 and x = 4 This means that a = 0 and b = 4 Evaluate both at 2 and observe which is greater y = 6(2)(2)^2 = 8 y = 2^2 2(2) = 0 The first one is greater so we subtract the second from the first in the integral int_0^4(6xx^2) (x^2 2x)dx Find the centroid of each simple region Replace each region with a point mass at its centroid, where the mass is the area of the region Find the centroid of these point masses (this is done by taking a weighted average of their x and y coordinates) This is easiest to see with an example ExampleRead how Numerade will revolutionize STEM Learning

How To Find Centroid Of A Parabolic Spandrel By Integration Youtube
Centroid of parabola y=x^2
Centroid of parabola y=x^2-Calculus Calculus Early Transcendental Functions Fluid Force on a Tank Wall In Exercises 914, find the fluid force on the vertical side of the tank, where the dimensions are given in feet Assume that the tank is full of water Parabola, y = x 2A 6 0 unit2 B 8 300 unit2 C 5 600 unit2 D 6 400 unit2 Part 2 What is the moment of inertia, about the Xaxis, of the area bounded by the parabola and the Xaxis?



How Do You Find The Area Between The Curves Y 4x X 2 And Y X Socratic
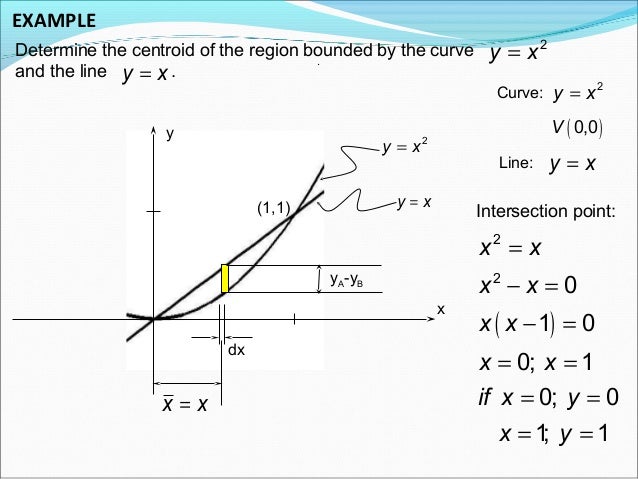
X = 1 A b a x (f (x)g (x)) dx 1 2 A b a (f (x) 2g (x) 2) dx Example Find the centroid of the region bounded by the line y = x and the parabola y = x 2 x 1 2 y 1 2 Solution Let f (x) = x and g (x) = x 2, a = 0 and b = 1The focus of a parabola can be found by adding to the xcoordinate if the parabola opens left or right Substitute the known values of , , and into the formula and simplify Find the axis of symmetry by finding the line that passes through the vertex and the focus Find the directrix The parabola \\(y=x^2\\\) has three points \\(P\_1,P\_2,P\_3\\\) on it The lines tangent to the parabola at \\(P\_1, P\_2, P\_3\\\) intersect each other pairwise at
Find the centroid of the region bounded by the curve x=2y^2 and the yaxis my work is shown below A= integral of (2y^2)dy from 0 toGet the free "Centroid y" widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Mathematics widgets in WolframAlphaFree Parabola calculator Calculate parabola foci, vertices, axis and directrix stepbystep This website uses cookies to ensure you get the best experience
A 15 045 000 unit4 B 18 362 000 unit4 C 11 100 000 unit4 D 21 065 000 unit4 Part 3 WhatThis engineering statics tutorial goes over how to find the centroid of the area under a parabola It requires a simple integrationIf you found this video hFind the centroid of a thin , flat plate covering the region enclosed by the xaxis, the lines x = 2 and x = 2, and the parabola y = x^2 Expert Answer 100% (1 rating)
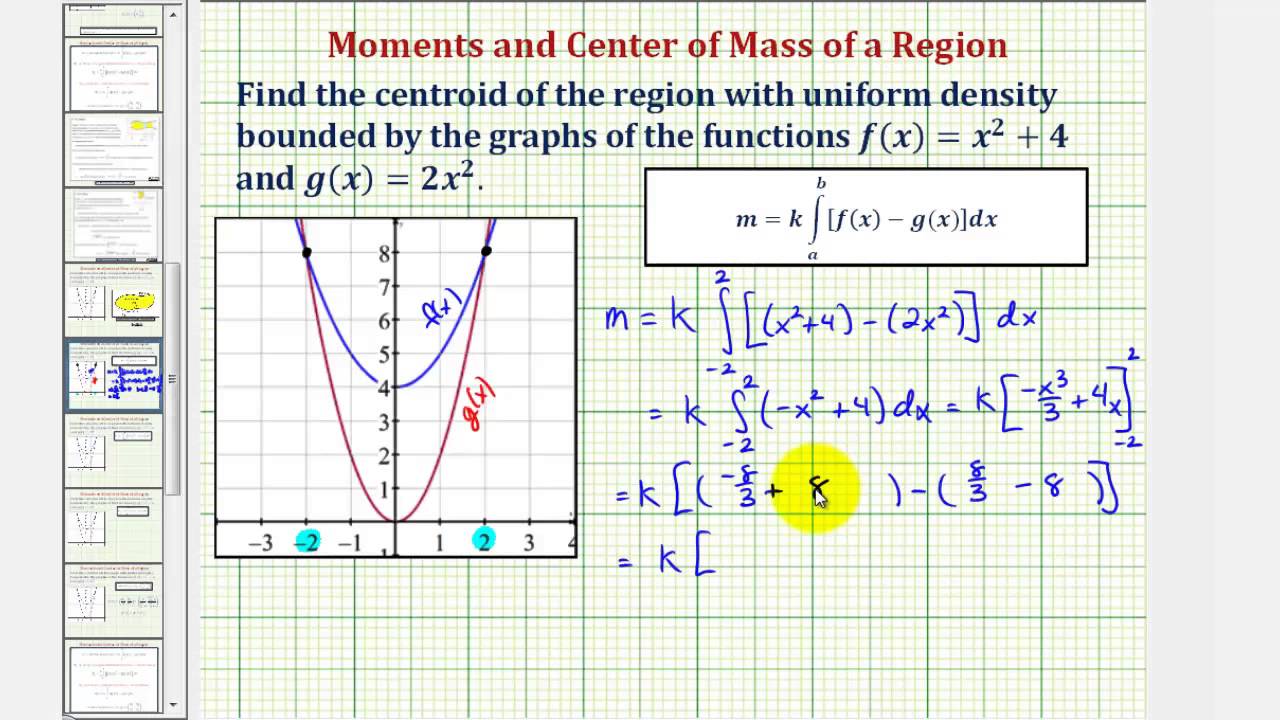



New Version Available Find The Centroid Of A Bounded Region Involving Two Quadratic Functions Youtube




Mechanics Map Centroid Of An Area
A hyperbolic paraboloid (not to be confused with a hyperboloid) is a doubly ruled surface shaped like a saddleIn a suitable coordinate system, a hyperbolic paraboloid can be represented by the equation 6 = In this position, the hyperbolic paraboloid opens downward along the xaxis and upward along the yaxis (that is, the parabola in the plane x = 0 opens upward and the parabola 0 votes centroid of parabolas x=y^2 and x^2=8y areaofparabolas asked in GEOMETRY by mathgirl Apprentice Please log in or register to add a comment I know I'm making this more difficult than it needs to be I need to find the centroid of a wire bent into the shape of a parabola, defined to be y=x^2 with 22 and 04
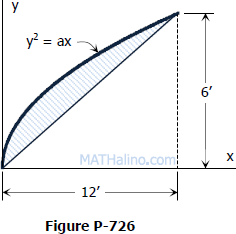



726 Area Enclosed By Parabola And Straigh Line Centroid Of Composite Area Engineering Mechanics Review At Mathalino



Physical Applications Of Double Integrals
The centroid of the triangle formed by the feet of three normals lies on the axis of the parabola The equation of the chord of the parabola y 2 = 4ax whose middle point is P(x 1 ,y 1 ) is yy 1 – 2a(x – x 1 ) = y 1 2 – 4ax 1Graph y=x^2 Find the properties of the given parabola Tap for more steps Rewrite the equation in vertex form Tap for more steps Complete the square for The directrix of a parabola is the horizontal line found by subtracting from the ycoordinate of the vertex if the parabola Get an answer for 'Find the centroid of the area bounded byx^2=4y ;




Find The Centroid Of The Area Bounded By The Parabola Y 4 X 2 And The X Axis Study Com




Upenn Math 114 Finding Centroid Of Region Bounded By Graphs Youtube
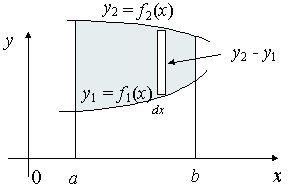
The centroid of the triangle formed by joining the feet of the normals drawn from any point to the parabola \{{y}^{2}}=4ax\, lies on MP PET 1999 A) Axis done clear find the centroid of the plane region bounded by the curves y = cos x, y=sinx, x=0, Math Find the centroid of the area in the first quadrant bounded by the curve y=e^x and the axes and the ordinate x=ln5 math The base of a solid is the region bounded by the parabolaThe y coordinate of the centroid is defined as ¯y = 1 2A ∫ b a ((yabove)2−(ybelow)2)dx= 1 2A ∫ b a ((f(x))2−(g(x))2)dx y ¯ = 1 2 A ∫ a b ( ( y a b o v e) 2 − ( y b e l o w) 2) d x




Solved X 2 A Y B Y Locate The Centroid Of The Parabolic Area X 2 A Y B 1 Answer Transtutors
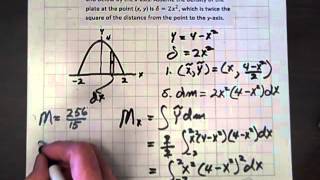



Calculate The Centroid Or Center Of Mass Of A Region Video Lessons Examples Step By Step Solutions
4 y y y y y y y y y y x x = − = − = = = = − = = Therefore, the intersection points are (0, 0) and (4, 2) Then lastly, say we have a parabola, just a standard y = x^2 It's centroid will be found on the y axis, but the exact value is only able to be determined by calculus I think I'm correct when I say that a section of parabola (made with a horizontal cut) will be similar to the parabola Find the coordinates of the centroid of the plane area bounded by the parabola y = 4 – x^2 and the xaxis Problem Answer The coordinates of the center of the plane area bounded by the parabola and xaxis is at (0, 16) Solution




Find The Centroid Of The Region Bounded By The Graphs Y X 2 Text And Y X Study Com



How Do You Find The Area Between The Curves Y 4x X 2 And Y X Socratic
Areas and Centroids b is the length of the member b b b b h h h h Nothing Nothing Curve Equation Shape Centroid (From Fat End of Figure) Area a x0 Straight Horizontal line Straight Sloping Line Parabola Cubic b/2 b/3 b/4 b/5 bh bh/2 bh/3 bh/4 To Solve For The Reactions 1) Draw a free body of the beam showing any actual distributed loadsQ 5411 Show that the coordinates of the centroid G of the area between the parabola y = x 2 a y = \frac {x^2} {a} y = ax2 and the straight line y = x are xAnswer to Find the centroid of the region bounded by the line y=x and the parabola y = x^2 By signing up, you'll get thousands of stepbystep




Find The Centroid Of The Region In The First Quadrant Chegg Com




Solution Locate The Centroid Of The Plane Area Bounded By The Parabola The Line And The X Axis
I'm proud to offer all of my tutorials for free If they have helped you then please consider buying me a coffee in return Other ways to support Engineer4FreeHow do you find the centre of gravity of the section of the parabola y=x^2 between y=100 and y= using integration?Question Find The Centroid Of The Region Bounded By The Line Y = 1 And The Parabola Y = X^2 This problem has been solved!




How To Find Centroid Of A Parabolic Spandrel By Integration Youtube




Find The Centroid Of The Region Bounded By The Parabola Y X 2 The Line X 2 And The X Axis Study Com
Y^2=4x (Area) Please show a graph or illustration and explain thoroughlyThank you enotes "NEED BADLY"' and find homework The center of mass or centroid of a region is the point in which the region will be perfectly balanced horizontally if suspended from that point So, let's suppose that the plate is the region bounded by the two curves f (x) f ( x) and g(x) g ( x) on the interval a,b a, b So, we want to find the center of mass of the region belowThe centroid of the triangle separates the median in the ratio of 2 1 It can be found by taking the average of x coordinate points and ycoordinate points of all the vertices of the triangle Centroid Theorem The centroid theorem states that the centroid of the triangle is at 2/3 of the distance from the vertex to the midpoint of the sides




Lesson 12 Centroid Of An Area
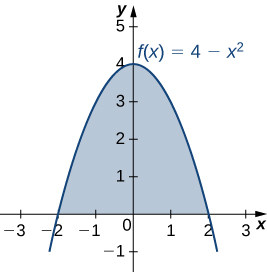



6 6 Moments And Centers Of Mass Calculus Volume 1
Centroid in rectangular coordinates = (04a, a) Centroid In polar coordinates $r = \sqrt{{\bar{x}}^2 {\bar{y}}^2} = \sqrt{(04a)^2 a^2}$ $r = \frac{\sqrt{29}}{5}a = 1077a$ $\theta = \arctan \left( \dfrac{\bar{y}}{\bar{x}} \right) = \arctan \left( \dfrac{a}{04a} \right)$ $\theta = ^\circ$ Centroid = (1077a, °) 2 x y= 2 8x y= −Determine the centroid of the area bounded by the parabolas and 2 x y= ( )0,0V Curve 1 dy y x (x1,y) (x2,y) (4,2) 2 x y= 2 8x y= − 2 1x x− x ( ),C x y y Curve 2 2 8x y= − ( )0,0V Solving for intersection points ( ) ( ) 2 2 4 4 3 8 8 8 0 8 0 0;Math 234,PracticeTest#3 Show your work in all the problems 1 Find the volume of the region bounded above by the paraboloid z = 9− x2−y2, below by the xyplane and lying outside the cylinder x2y2 = 1 2 Evaluate the integral by changing to polar coordinates




Mechanical Engineering Centroids Center Of Gravity 11 Of 35 C G Of A General Spandrel 1 Youtube



Http Faculty Mercer Edu Jenkins He Documents Centroids Pdf
Find the coordinates of the centroid of the plane area bounded by the parabola y = 4 – x^2 and the xaxis Contribute to PinoyBIX Community either by Asking question or Answering then Share it to Social Media!!! Find the centroid of the area bounded by the parabola y=4x^2 and the xaxis A(0,16) B(0,17) C(0,18) D(0,19) CALCULUS Sketch the region enclosed by the given curves y = 4/X y = 16x, y = 1X/16 x > 0 and the area between the curves CALCULUSSituation Given the parabola 3x2 40y – 4800 = 0 Part 1 What is the area bounded by the parabola and the Xaxis?



What Is The Centroid Of The Solid Formed By Revolving The Region Bounded By Y 4 X 2 And Y X And X 0 About Y Axis Quora
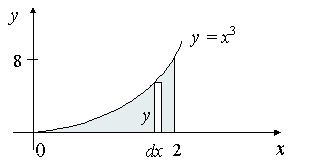



5 Centroid Of An Area By Integration
Question What is the area bounded by the parabola y^22x2y3 =0 and the yaxis?Solution Find the coordinates of the centroid of the plane area bounded by the parabola and xaxis Solution Locate the centroid of the plane area bounded by y = x^2 and y = x Solution Find the area of the curve r^2 = a^2 cos 2θCentroid of a semiparabola Find the coordinates of the centroid of a parabolic spandrel bounded by the \(y\) axis, a horizontal line passing through the point \((a,b),\) and a parabola with a vertex at the origin and passing through the same point \(a\)




Calculus Ii Lesson 7a Applications Of Integration 6 Centroids Application Center



1
Centroid lies on that axis •If an area possesses two lines of symmetry, its centroid lies at their intersection •An area is symmetric with respect to a center O if for every element dA at (x,y) there exists an area dA' of equal area at (x,y) •The centroid of the area coincides with the center ofCentroid x Added by htmlvb in Mathematics Calculates the x value of the centroid of an area between two curves in bounds a, b8 Find the center of mass and the moment of inertia and radius of gyration about the yaxis of a thin plate bounded by the line y = 1 and the parabola y = x 2 if the density is δ (x, y) = y 1 (Ans centroid (0, 9 14), I y = 16 35, R y = q 3 14) 9 Calculate centroid of the area bounded by the parabola x 2 4 y16 = 0 and xaxis (Ans



Http Faculty Mercer Edu Jenkins He Documents Centroids Pdf
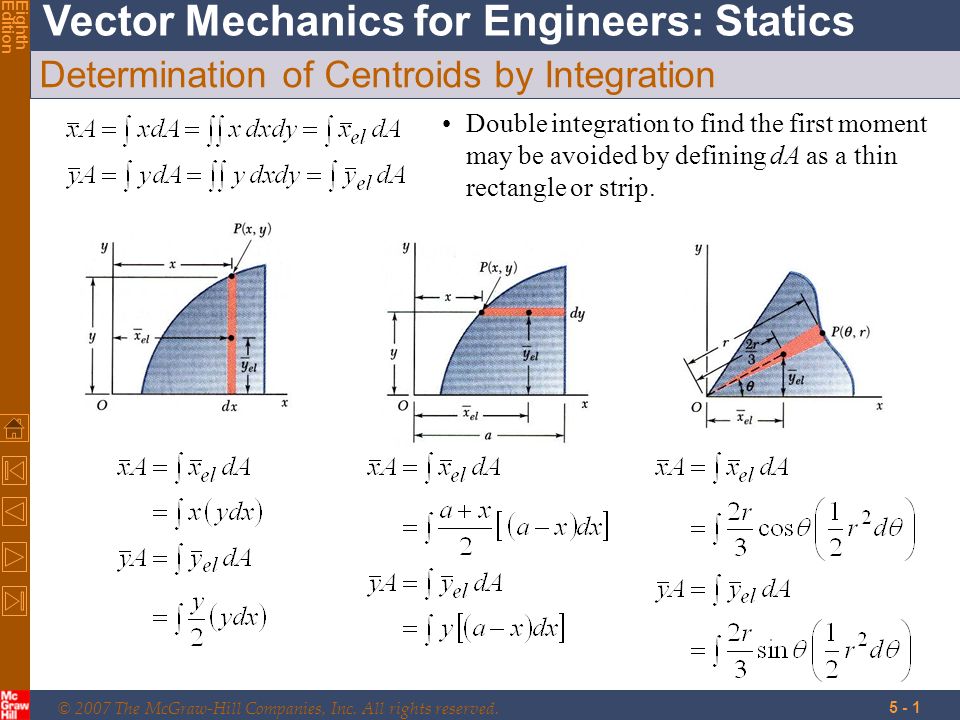



Determination Of Centroids By Integration Ppt Video Online Download
The centroid of a plate R that is bounded by the curves f (x) and g (x) where f (x) ≥ g (x) is located at (x, y) where;Locate the centroid of the circular arc Solution Polar coordinate system is better Since the figure is symmetric centroid lies on the x axis Differential element of arc has length dL = rd Total length of arc L = 2 αr xcoordinate of the centroid of differential element x=rcos For a semicircular arc 2α= π centroid lies at 2 r/π L zdL I was looking for the centroid of the area bounded by the curves y = x 2 − 4 and y = 2 x − x 2 My work I visualize the problem like this Using the vertical strip d x and remembering that the centroid C ( x ¯, y ¯) can be found by the formula A x ¯ = ∫ x c d A and A y ¯ = ∫ y c d A Now getting the A, x c, d A, and y c To get
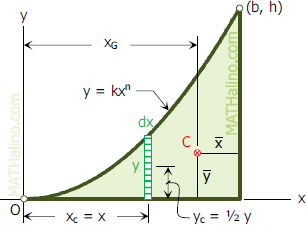



708 Centroid And Area Of Spandrel By Integration Engineering Mechanics Review At Mathalino
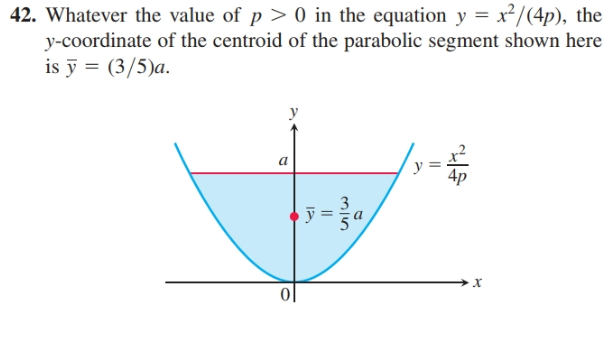



Answered 42 Whatever The Value Of P 0 In The Bartleby
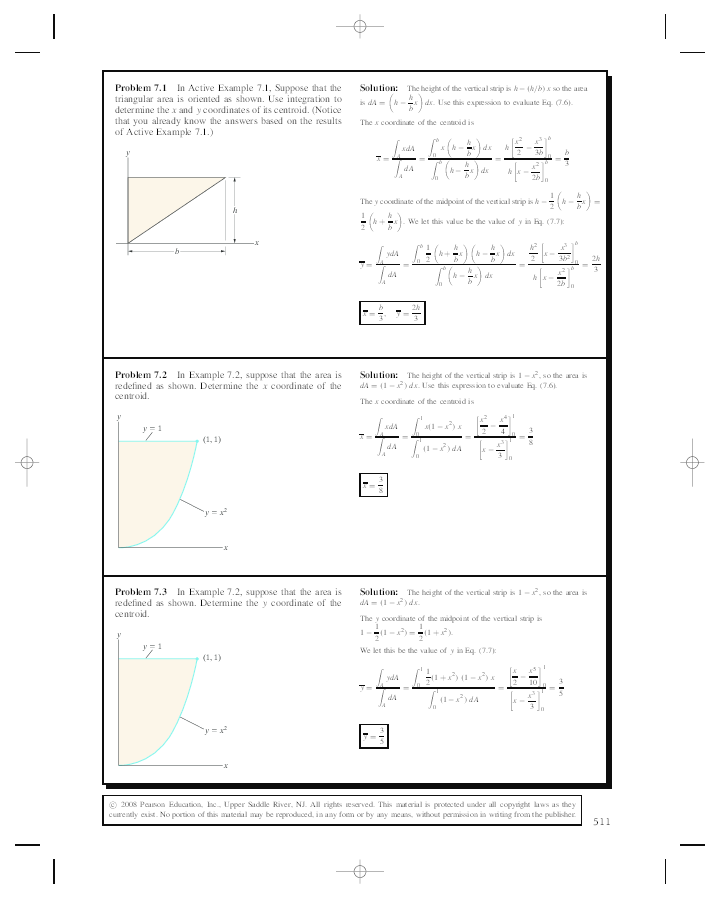
How to find the centroid of the area under a parabola 5/4/17 Comments are closed Hello!Let coordinates of the centroid be (h, k) (0,3) from parabola y = x 2 is q p Find the position of point (2, 4) with respect to y = x 2 View Answer State the following statement is True or False The parabola f (x) = a x 2 b x c does not touch or intersect with the x axis if b 2 < 3Remember that the x i is the xdistance to the centroid of the ith area 1 1 n ii i n i i xA x A = = = ∑ ∑ 33 Centroids by Integration Wednesday, Centroids from Functions !
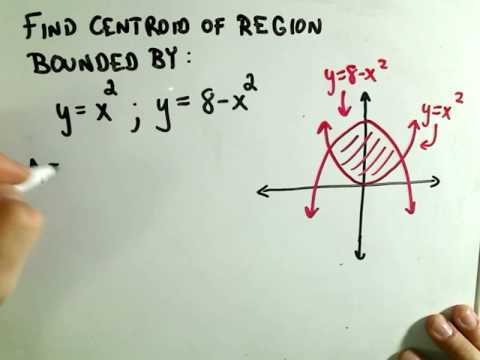



Centroids Centers Of Mass Part 1 Of 2 Youtube




Answered 5 Locate The Coordinates Of The Bartleby
Find the centroid of the region in the first quadrant bounded by the curves given by 4 y=x^{2}, x=0, and y=4 🎉 Announcing Numerade's $26M Series A, led by IDG Capital!Solve for x math2x = y^2 2y 3/math Find where the yintercepts let x = 0, mathy^2 2y 3 = 0/math, therefore mathy = 3/math and mathy = 1 /mSee the answer Show transcribed image text Expert Answer Previous question Next question Transcribed Image Text from this Question




Find A Center Of Mass Of A Thin Plate Of Density 8 Chegg Com




Centroid Area Moments Of Inertia Polar Moments Of Inertia Radius Of Gyration For The First Quadrant Of A Parabolic Area
You take moments But first you have to decide which section you are interested in There is a branch between mathx=10/math tSo far, we have been able to describe the forces (areas) using rectangles and triangles !Now we have to extend that to loadings and areas
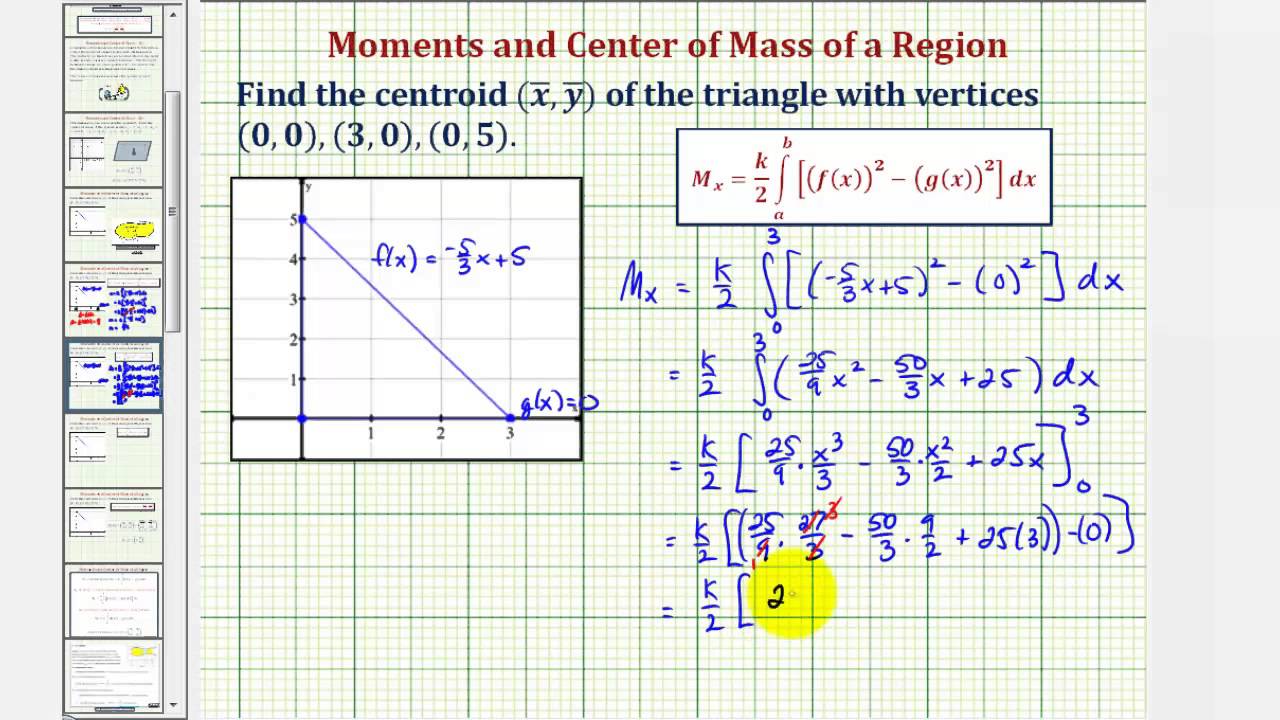



Calculate The Centroid Or Center Of Mass Of A Region Video Lessons Examples Step By Step Solutions




Finding The Centroid Of The Planar Region Bounded By The Parabola Y 4 X 2 And The Line Y X 2 Study Com
Since the parabola is in the form $x^2 = 4ay$ where $a=9$, I deduced that the vertices of the triangle will be $A(9t_1^2,18t_1)$, $B(9t_2^2,18t_2)$ and $C(9t_3^3,18t_3)$ The $x$ and $y$ coordinates of centroid $h$ and $k$ will thus be given by the sum of coordinates of the vertices $h = 6(t_1t_2t_3)$ and $y = 3(t_1^2t_2^2t_3^2)$




Find The Center Of Gravity Centroid Of The Region R Enclosed Between The Curves Y X 2 And Y X 6 Study Com



Http Www Iitg Ac In Rkbc Me101 Presentation L16 18 Pdf



1



Anvari Net Dynamics Chapter 9 Pdf




Solution Locate The Centroid Of The Plane Area Bounded By Y X 2 And Y



Find The Exact Coordinates Of The Centroid Mathskey Com




15 6 Calculating Centers Of Mass And Moments Of Inertia Mathematics Libretexts




Lesson 12 Centroid Of An Area




Find The Coordinates Of The Centroid Of The Plane Gauthmath




List Of Centroids Wikipedia



What Is The Centroid Of The Solid Formed By Revolving The Region Bounded By Y 4 X 2 And Y X And X 0 About Y Axis Quora
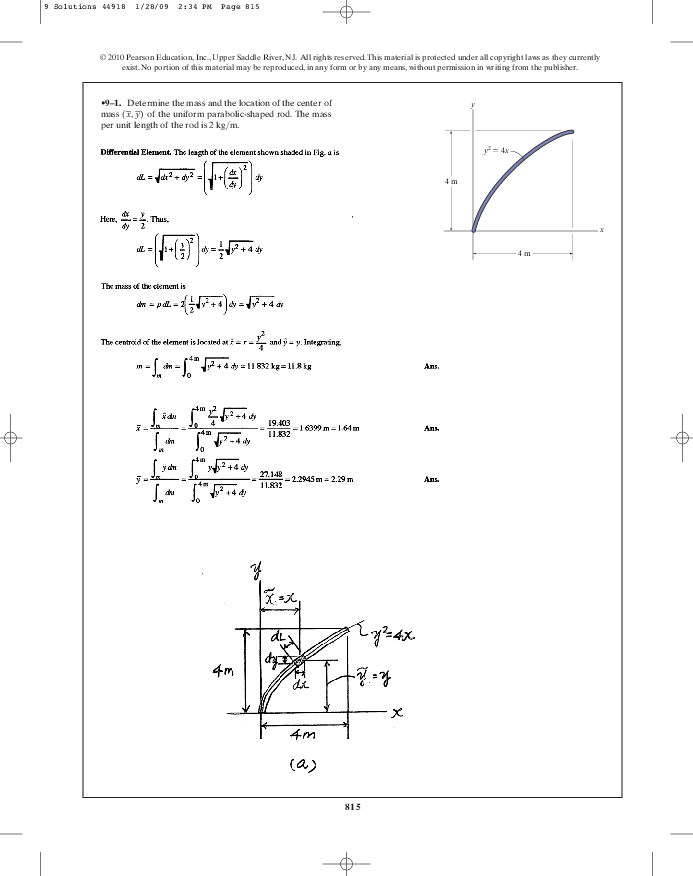



Pdf Chapter 9 Rafey Imtiaz Academia Edu



1
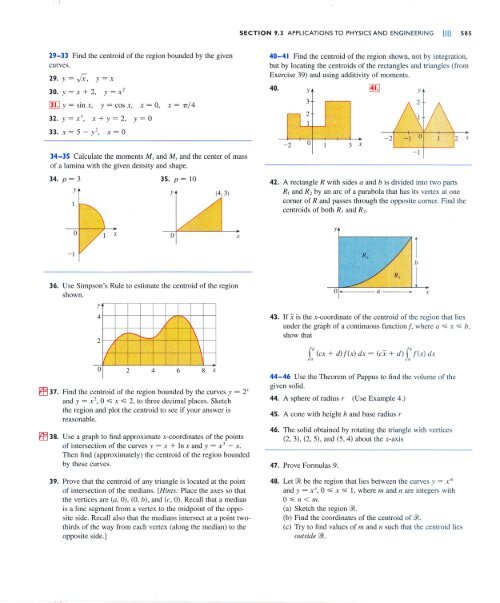



12 A Large Tank Is Desig
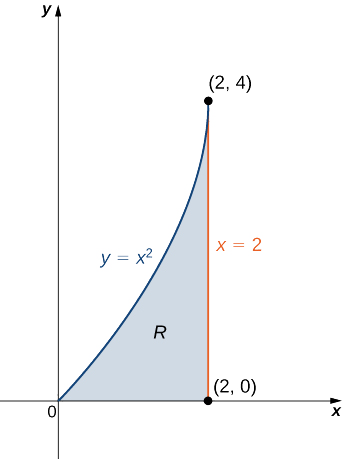



15 6 Calculating Centers Of Mass And Moments Of Inertia Mathematics Libretexts




Solution Locate The Centroid Of The Plane Area Bounded By Y X 2 And Y X




Centroids Reference Table Calcresource
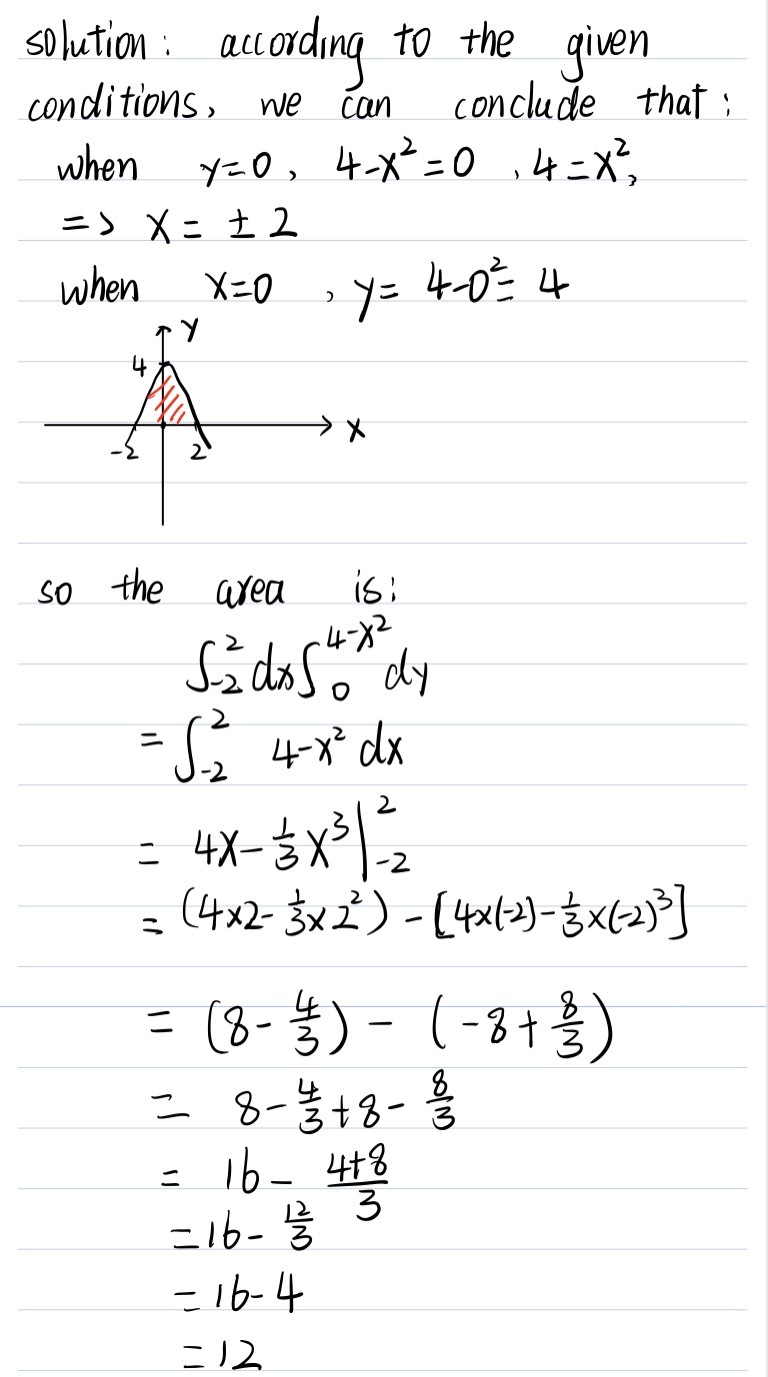



Find The Coordinates Of The Centroid Of The Plane Gauthmath
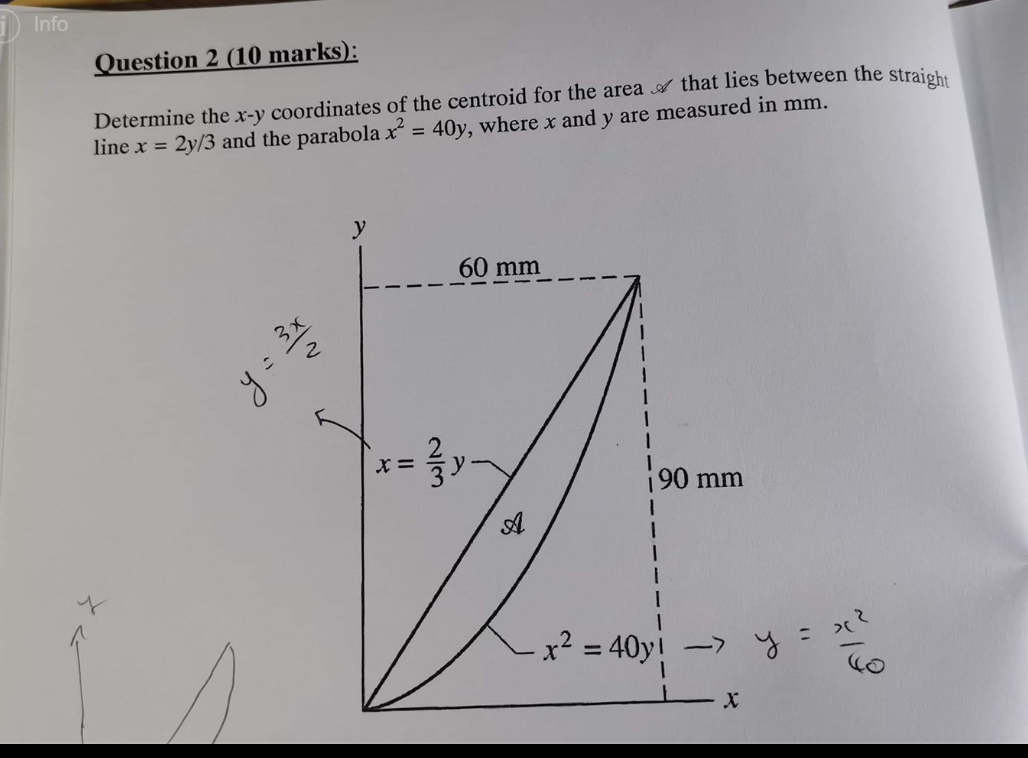



Info Question 2 10 Marks Determine The X Y Chegg Com




Determine The Centroid X Y Of The Shaded Area Youtube



What Is The Centroid Of The Area Under Y 4 X In The First Quadrant And Graph It Quora



Http Www Rpi Edu Dept Core Eng Www Iea F15 Lectures Lecture17 Pdf
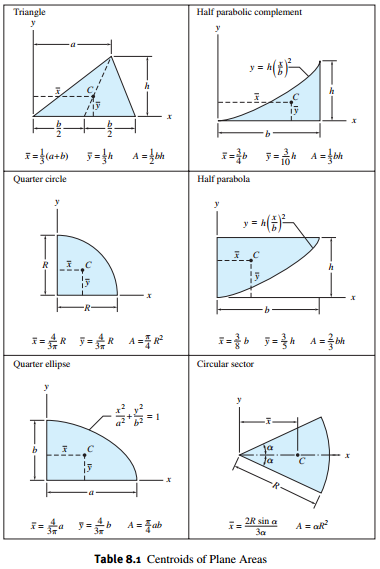



Solved A Using Integration Locate The Centroid Of The Area Under The 1 Answer Transtutors




How To Find The Centroid Of The Area Under A Parabola Youtube




8 Further Applications Of Integration Further Applications Of




List Of Centroids Wikipedia
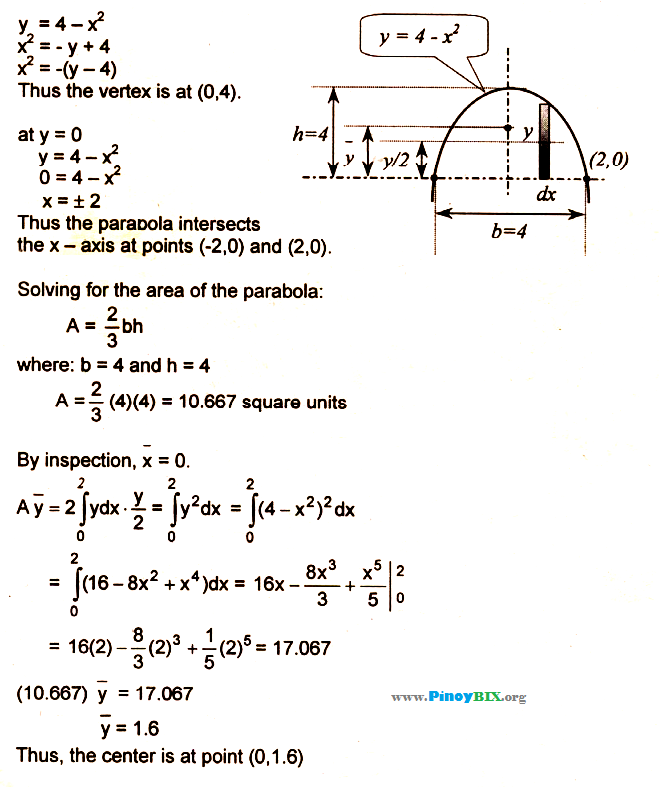



Solution Find The Coordinates Of The Centroid Of The Plane Area Bounded By The Parabola And




Find The Centroid Of The Region The Triangle With Chegg Com




Locate The Centroid X Bar Of The Parabolic Area Enclosed By The Curve Y H X 2 A 2 The Line X A And Y H Take A 8 In And H 10 In Study Com




Ch09h Problem 9 16 Locate The Centroid Of The Shaded Area Bounded By The Parabola And The Line Y A Solution 3 A A 0 2 2 Xc 2 2 A 3 A 2 A 1 3 A Y Course Hero




Ch09h Problem 9 16 Locate The Centroid Of The Shaded Area Bounded By The Parabola And The Line Y A Solution 3 A A 0 2 2 Xc 2 2 A 3 A 2 A 1 3 A Y Course Hero




Find The Centroid Of The Region Bounded By The Line Y X And The Parabola Y X 2 Study Com



Parabolic Segment From Wolfram Mathworld



5 Centroid Of An Area By Integration



Pdf Statics Bedford Chap Daniela Ubaque Garcia Academia Edu



Lesson 12 Centroid Of An Area
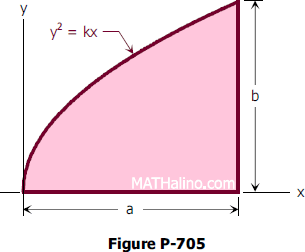



705 Centroid Of Parabolic Segment By Integration Engineering Mechanics Review At Mathalino
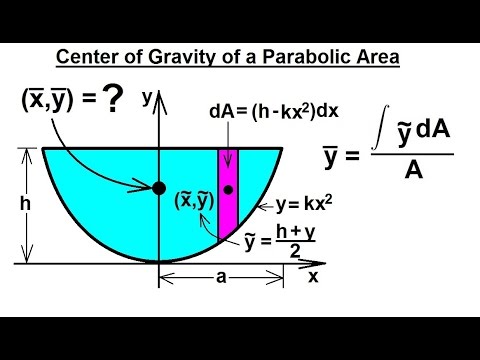



Mechanical Engineering Centroids Center Of Gravity 9 Of 35 C G Of A Parabolic Area Youtube



Whatever The Value Of P 0 In The Equation Y Chegg Com



5 Centroid Of An Area By Integration




Solved Locate The Centroid Of The Parabolic Area X Overbar A 3 2 Answers Transtutors




Find The Centroid Of The Region Bounded By The Parabolas Y X 2 4 And Y 0 75x 2 3 Study Com
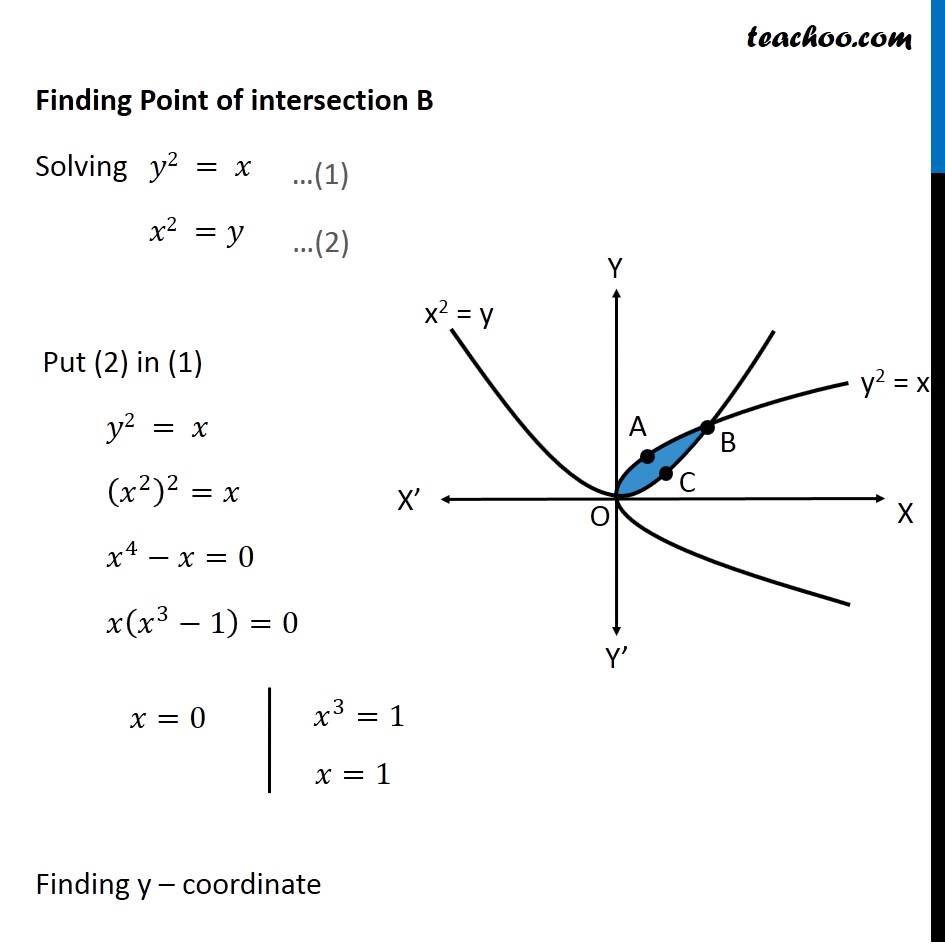



Example 6 Find Area Bounded By Two Parabolas Y X2 Y2 X




Mechanical Engineering Centroids Center Of Gravity 10 Of 35 C G Of A Parabolic Spandrel Youtube




Find The Centroid Of The Region Bounded By The Curves Y 2x X 2 Y 1 X 0 Assume Uniform Density Rho The Shape Is A Parabolic Spandrel Study Com




Solution Locate The Centroid Of The Plane Area Bounded By The Parabola The Line And The



Http Www Rpi Edu Dept Core Eng Www Iea F15 Lectures Lecture17 Pdf
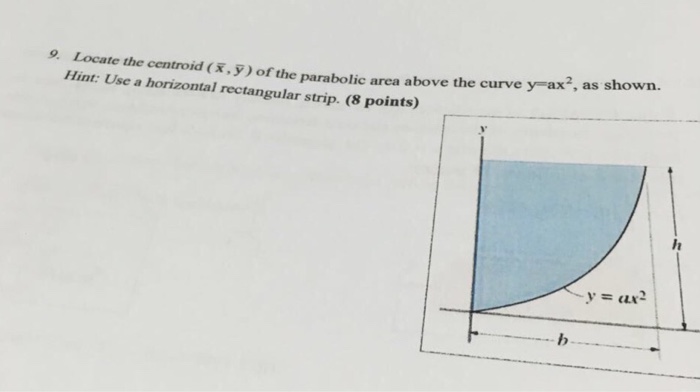



Locate The Centroid X Y Of The Parabolic Area Chegg Com



Center Of Mass And Moments
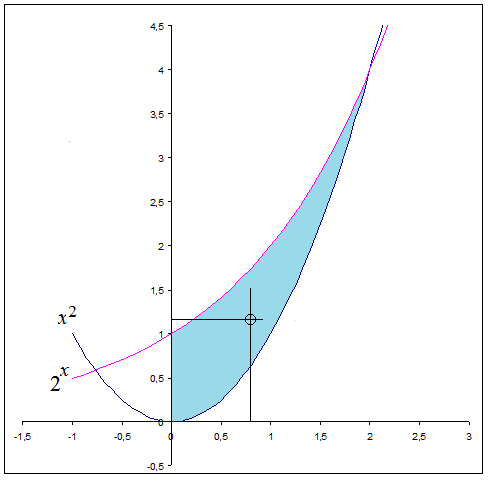



Find Centroid Of Region Of Two Curves Mathematics Stack Exchange




Lesson 12 Centroid Of An Area




List Of Centroids Wikipedia




What Is The Area Of The Region Bounded By The Parabola Y 2 4x And The Line X 1 Quora




Centroid Of Volume Bounded By A Line And A Parabola Mathematics Stack Exchange




Centroid Analysis Module Vccs Engineering Bridge Modules
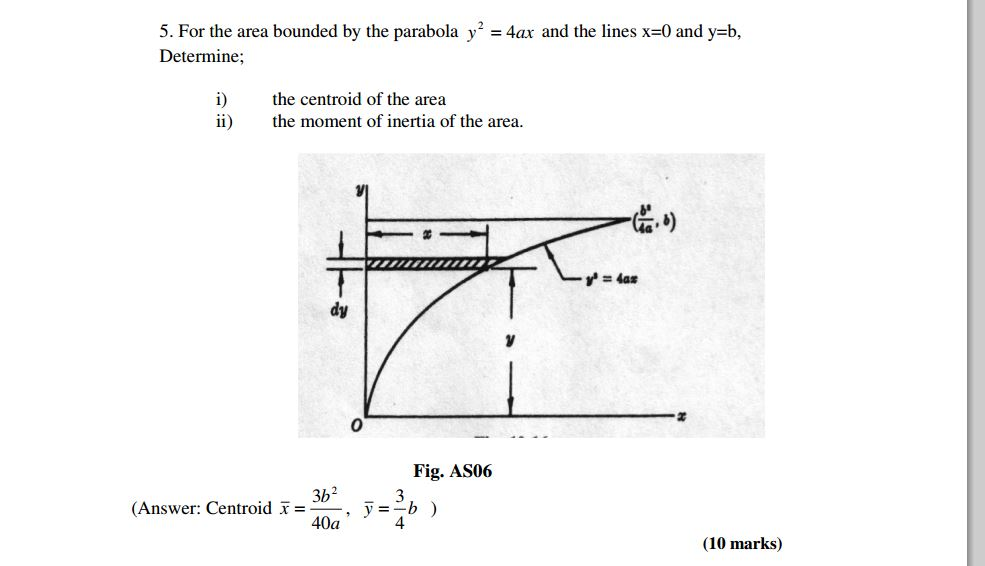



5 For The Area Bounded By The Parabola Y 2 4ax And Chegg Com



Solved Find The Centroid Of The Area Bounded By The Parabolas X2 Y And Y 9 Course Hero



Anvari Net Dynamics Chapter 9 Pdf




Solution Find The Coordinates Of The Centroid Of The Plane Area Bounded By The Parabola And X Axis
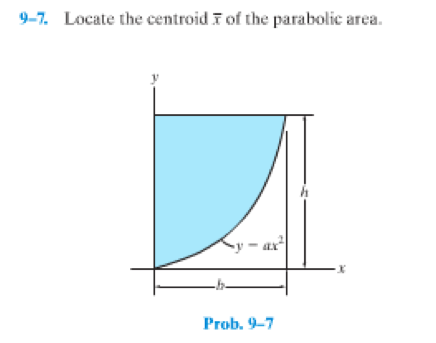



Locate The Centroid X Of The Parabolic Area Chegg Com




3 Moment And Center Of Mass Centroid Find The Chegg Com
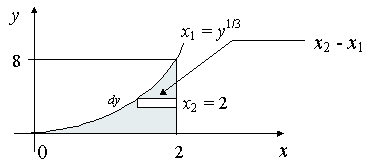



5 Centroid Of An Area By Integration
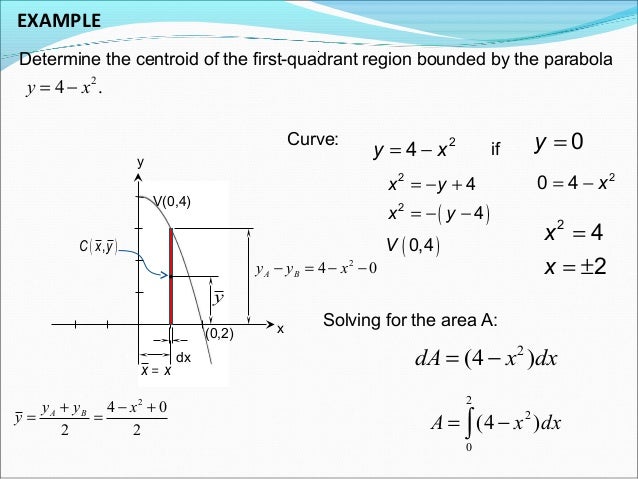



Lesson 12 Centroid Of An Area
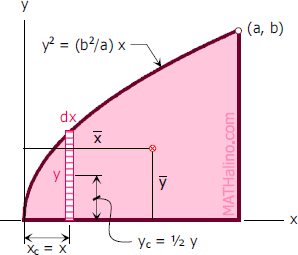



705 Centroid Of Parabolic Segment By Integration Engineering Mechanics Review At Mathalino
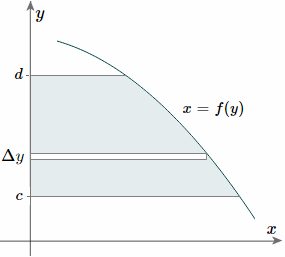



5 Centroid Of An Area By Integration



Mechanics Map Centroid Of An Area




Centroid Of Area By Integration Spr18 Youtube
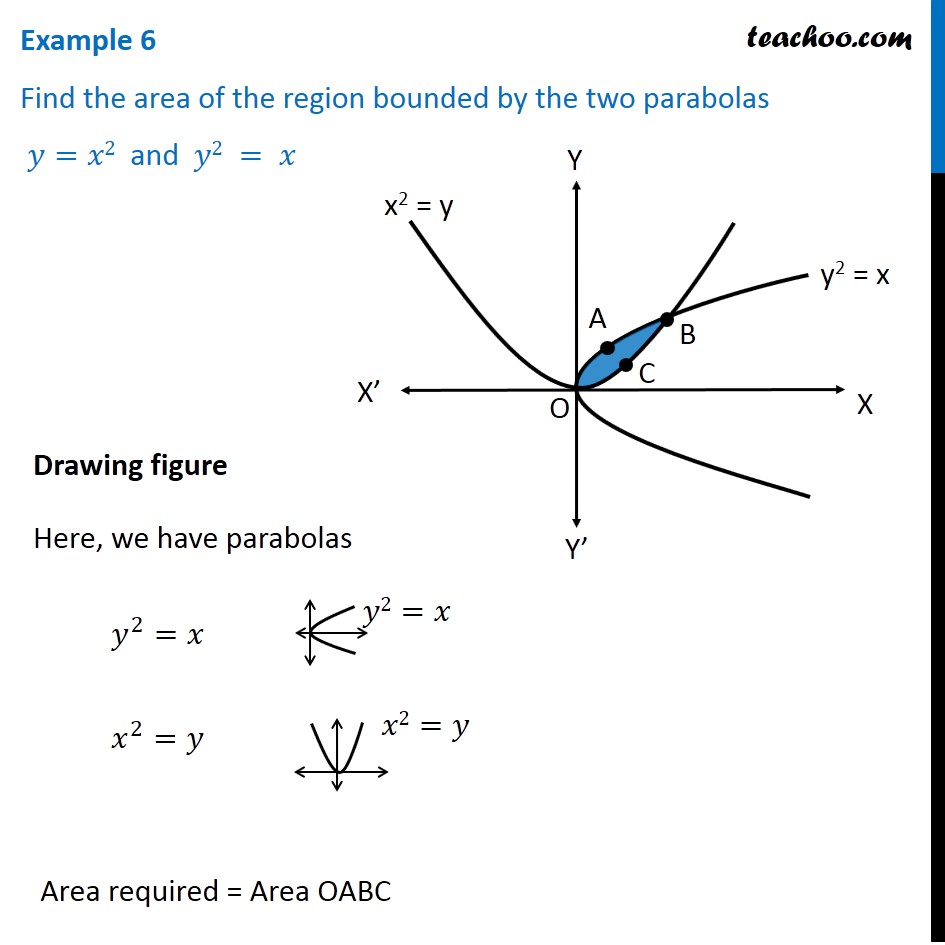



Example 6 Find Area Bounded By Two Parabolas Y X2 Y2 X




Find The Centroid Of The Area Bounded By The Parabola Chegg Com



Pappus S Theorem



Q Tbn And9gcrwvb4aso6v3vuqob5s F Fllw1kz X6tm6ggg6fvpe7bm0m2y9 Usqp Cau




List Of Centroids Wikipedia



0 件のコメント:
コメントを投稿