Integrate both sides again v = C1 4 x4 C2 Now the general solution is given as y2 = v(x)y1 y2 = ( C1 4 x4 C2)( 1 x) y2 = (C1( x3 4) C2( 1 x)) Now the first solution is given when C1 = 0, then the second solution can be when C2 = 0 which is x3 4 otherwise there are infinite solutionsby just filling the constants To checkMathx=s3t/math math\frac{d}{ds}x^2=\frac{d}{ds}(s3t)^2/math math=2(s3t)/math math\frac{d^2}{ds^2}x^2=\frac{d}{ds}(\frac{d}{ds}x^2)/math mathFunction equal to each other so there is no extra X or Y being consumed that gives no extra utility 2X=3Y rearrange Y=2X/3 – so ray from original which goes through all the corners of the L has to have the slope 2/3 The indifference curve is for when utility is 6 y 3 X 2 Ray from the origin slope is 2/3 U
Www Ualberta Ca Csproat Homework Math 334 Assignment solutions Assignment 2 solutions Pdf
If u(x y)=x^2 y^2 2x-3xy then
If u(x y)=x^2 y^2 2x-3xy then-2x 3 y 2 4x 2 y 2 = 2x 2 y 2 • (x 2) Adding fractions that have a common denominator Adding up the two equivalent fractions Add the two equivalent fractions which now have a common denominator Combine the numerators together, put the sum or difference over the common denominator then reduce to lowest terms if possible What is the value of the expression 2x^23xy4y^2 when x = 2 and y = 4?



1
I got mu(y) = e^y The point of an integrating factor is to turn an inexact differential into an exact one One physical application of this is to turn a path function into a state function in chemistry (such as dividing by T to turn q_"rev", a path function, into S, a state function, entropy) I assume that the second terms include 3y^2, not 3y (it would be odd to not simply write 9y)52 f(x;y) = C This is because the di erential equation can be written as df= 0 Here we will not develop the complete theory of exact equations, but will simply give examples of how they are dealt with Example Find the general solution to (3x2y2 3y2)dx (2x3y 6xy 3y2)dy= 0 Step 1 Check to see if M y = N x M= 3x2y2 3y2 Consider the equation x^2 2xy 4y^2 = 64 Write an expression of the slope of the curve at any point (y^p)= y prime My work 2x 2(xy^p y) 8yy^p = 0 2x 2xy^p 2y 8yy^p = 0 2xy^p 8yy^p = 2y 2x factored out y^p and You can view more similar questions or
The differential equation dy/dx xy/(1x^2) = xy^1/3 is a Bernulli equation which can be reduced to normal form taking y = V(x)^3/2 So y' = (3/2)(V^1/2)V' and the equation becomes V' (2/3)xV/(x^2–1) = 2x/3 The integrating factor is e^IntegI wonder there is a precalculus method, without using the Lagrange multiplier The function is not harmonic, so it cannot have a conjugate On the other hand, if we fix the example as u(x, y) = x3 2xy − 3xy2, then ux = 3x2 2y − 3y2 uxx = 6x uy = 2x − 6xy uyy = − 6x and this u is harmonic The harmonic conjugate v must satisfy vx = − uy vy = ux Thus vx = − 2x 6xy vy = 3x2 2y − 3y2 Hence v = − x2
Find dy/dx x2xyy^2=2 Differentiate both sides of the equation Differentiate the left side of the equation Tap for more steps Differentiate Tap for more steps By the Sum Rule, the derivative of with respect to is Differentiate using the Power Rule which states that is whereStep by step solution Consider 2x^ {2}3xy2y^ {2}2x11y12 as a polynomial over variable x Find one factor of the form kx^ {m}n, where kx^ {m} divides the monomial with the highest power 2x^ {2} and n divides the constant factor 2y^ {2}11y12 One such factor is 2xy4 Factor the polynomial by dividing it by this factorDy/dx= (2x3y1)/(3x2y1) Let x= Xp and y = Yq then dy/dx = dy/dX dy/dX= (2X2p3Y3q1)/(3X3p2Y2q1) = dy/dX = {2X3Y(2p3q1)}/{3X2Y(3p2q1)} Now 2p




100以上 If U X Y X 2 Y 2 2x 3xy Then 1764 Josspix7odk
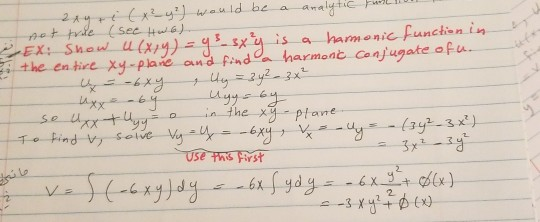



Exercises 1 Show That U X Y Is Harmonic In Some Chegg Com
Question 3 Kanghyock Has Preferences Given By U(x,y) = 3xy 2x Y, And An Income Of 1 = 102 Prices Are Given By P = 1, Py = 2 Solve For His Optimal Consumption Bundle If x=32√2 and xy=1, then (x²3xyy²)/(x²3xyy²) 122Equations Tiger Algebra gives you not only the answers, but also the complete step by step method for solving your equations 4x^2y^2/2x^23xy2y^2^22xy/xy2x^2 so that you understand better



Web Williams Edu Mathematics Sjmiller Public Html 150 Hwsolns Hwsolns Math150 Sp14 Pdf




If 2x 2 3xy Y 2 X 2y 8 0 Then Dy Dx Youtube
Subtract 2x from each side to get y=2x2 Now substitute this expression for y into the second equation 3x2y=5 3x2(2x2)=5 solve for x 3x4x4=5x=1 ==> x=1 If x=1 then y=2(1)2=4 So(x^2–2xyy^2)dx = (y^22xyx^2)dy =>dy/dx = (x^2–2xyy^2)/((x^22xyy^2)(1) Let y = vx => dy/dx = v xdv/dx (1) becomes v xdv/dx = (x^2–2x^2vv^2x^2Solve for y x^23xyy^2=1 Move to the left side of the equation by subtracting it from both sides Use the quadratic formula to find the solutions Substitute the values , , and into the quadratic formula and solve for Simplify Tap for more steps Simplify the numerator Tap for more steps




If 4x 2 Xy 3xy Y 2 12 5 Find X 2y 2x Y Brainly In




4 Given The Function F X Y 4 X2 Y3 3xy A Find All Critical Points Homeworklib
Integrating Factors Some equations that are not exact may be multiplied by some factor, a function u (x, y), to make them exact When this function u (x, y) exists it is called an integrating factor It will make valid the following expression ∂ (u·N (x, y)) ∂x = ∂ (u·M (x, y)) ∂yFor any unit vector, u =〈u x,u y〉let If this limit exists, this is called the directional derivative of f at the point (a,b) in the direction of u Theorem Let f be differentiable at the point (a,b) Then f has a directional derivative at (a,b) in the direction of u u = u xi u yj and D u f(a,b) = uLemma 54 Let z= x iyand suppose that f(z) = u(x;y) iv(x;y) is analytic Then the dot product of their gradients is 0, ie rurv= 0 Proof The proof is an easy application of the CauchyRiemann equations rurv= (u x;u y) (v x;v y) = u xv x u yv y= v yv x v xv y= 0 In the last step we used the CauchyRiemann equations to substitute v yfor



The Two Curves X 3 3xy 2 2 0 And 3x 2y Y 3 2 0 Youtube



Www Pnw Edu Wp Content Uploads 03 Lecture Notes 8 5 Pdf
Definition 161 Suppose H R2 → R has continuous second partial deriva tives on a domain D We say H is harmonic in D if for all (x,y) ∈ D, H xx(x,y)H yy(x,y) = 0 Harmonic functions arise frequently in applications, such as in the study Use the power rule, dy/dx = nx^ (x1) d y d x = n x x − 1 , on the first term 2x (3d (xy))/dx (d (y^2))/dx= (d (0))/dx 2 x 3 d ( x y) d x d ( y 2) d x = d ( 0) d x Use the product rule, (d (xy))/dx= dx/dxyxdy/dx = y xdy/dx d ( x y) d x = d x d x y x d y d x = y x d y d xMATH 106 HOMEWORK 3 SOLUTIONS 1 Using the CauchyRiemann equations, show that if f and f are both holomorphic then f is a constant Solution Let f = uiv,so f = u iv Since they are holomorphic, we can use the CauchyRiemann




If U Sin 1 X 2 Y 2 X Y Then Show That X Du Dx Y Du Dy Tan U Mathematics 1 Question Answer Collection




If 2x 2 3xy Y 2 X 2y 8 0 Then Dy Dx
We think you wrote (3x)/(2x^23xy2y^2)(y)/(x^24y^2)(2xy)/(2x^25xy2y^2) This deals with adding, subtracting and finding the least common multipleIf u x log xy where x 3 y 3 3xy 1 then du is dx a 2 2 x x y 1 log xyy y x b 2 2 from AA 1 CS314Lecture28 Introduction to Frequency Response Designpdf Stellenbosch UniversitySouthIf 3 sin (xy) 4 cos (xy) = 5, then dy/dx = If 3 Tan Theta Tan Phi Is 1 Then If 3 x = 4 x1, then x is equal to If 3x y k = 0 is a tangent to the circle x 2 y 2 = 10, then the values of k are If 4 Sin Inverse X Plus Cos Inverse X Pi Then X Is If 5 9 13 N Terms 7 9 11 12 Terms 5 12 Then N Equals




Worked Example Implicit Differentiation Video Khan Academy



Http Edshare Soton Ac Uk Id Document 4796
What is the maximum of $x^23xy2y^2$ subjects to $x^2xyy^2=1$?All equations of the form a x 2 b x c = 0 can be solved using the quadratic formula 2 a − b ± b 2 − 4 a c The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction x^ {2}2xy^ {2}4y=5 x 2 − 2 x y 2 − 4 y = The factored form is (x3y)(xy) You can treat it like a quadratic, where instead of constant numbers, there are y terms First, find two numbers that multiply to 3 (the c value of the "quadratic") and add up to 2 (the b value of the "quadratic") These two numbers are 3 and 1 Split the middle term into these two numbers Then, factor the first two and last two terms separately, then



Www Ualberta Ca Rjia Math214 Hwks Sol10 Pdf




7 05 Rotated Conics
Subject to the constraint 2x2 (y 1)2 18 Solution We check for the critical points in the interior f x = 2x;f y = 2(y1) =)(0; If u = x^3 3xy^2 y^3 then ∂^2u/∂y∂x is (a) 3 (b) 6y (c) 6x (d) 2 asked in Applications of Differentiation by Darshee ( 491k points) applications of differentiationC M K Warby MA3614 Complex variable methods and applications 5 Partially integrating with respect to xgives v(x;y) = x 2xy 2x2 g(y) where g(y) is any di erentiable function of y




100以上 If U X Y X 2 Y 2 2x 3xy Then 1764 Josspix7odk



Faculty Math Illinois Edu G Choi1 242review2 Sol Pdf
1) is a critical point The second derivative test f xx = 2;f yy = 2;f xy = 0 shows this a local minimum withSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreFactor 2x^23xyy^2 2x2 3xy y2 2 x 2 3 x y y 2 For a polynomial of the form ax2 bx c a x 2 b x c, rewrite the middle term as a sum of two terms whose product is a⋅c = 2⋅1 = 2 a ⋅ c = 2 ⋅ 1 = 2 and whose sum is b = 3 b = 3 Tap for more steps Reorder terms 2 x 2 y 2 3 x y 2 x 2 y 2 3 x y Reorder y 2 y 2 and 3



Web Ma Utexas Edu Users Rav M408d F10 M408d Quiz6 Solutions Pdf



How To Solve Math X 3 Y 3 Dx 3xy 2dy 0 Quora
If the lines represented by the equation 2x^2 3xy y^2 = 0 make angles α and β with xaxis, then cot^2 α cot^2 βI read the following equation M(x,y)dx N(x,y)dy =0 , with M(x,y) = y(y 2x 2 ) , N(x,y) = 2(x y) The equation is not exact because M_y =2(x y 1) # N_xCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history



Jntua Ac In Gate Online Classes Registration Downloads Material A Pdf



Www3 Nd Edu Taylor Math550 Images Worksheets Solutions05 Pdf
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreQUESTIONShowthatu(x;y) = 2x¡x33xy2 isharmonic Findaconjugate harmonic function v(x;y) and identify the corresponding analytic function uiv ANSWER Easy to show uxx uyy = 0, so u is harmonic Let v be the conjugate harmonic function Then vy = ux = 2¡3x2 3y2 Thus v(x;y) = 2y¡3x2yy3 `(x) Now vx = ¡6xy`0(x) = ¡uy = ¡6xy Thus `(xQuestion Show That U(x, Y)2xx 3xy2 Is Harmonic Find The Hamonic Conjugate V(x,y) Of U(x,y)·Then Construct The Analytic Function F(z) = U(x, Y) IV(x, Y) Satisfying F (2i) 23i




Ex 9 5 15 Class 12 Find Solution 2xy Y 2 2x 2 Dy Dx 0 When
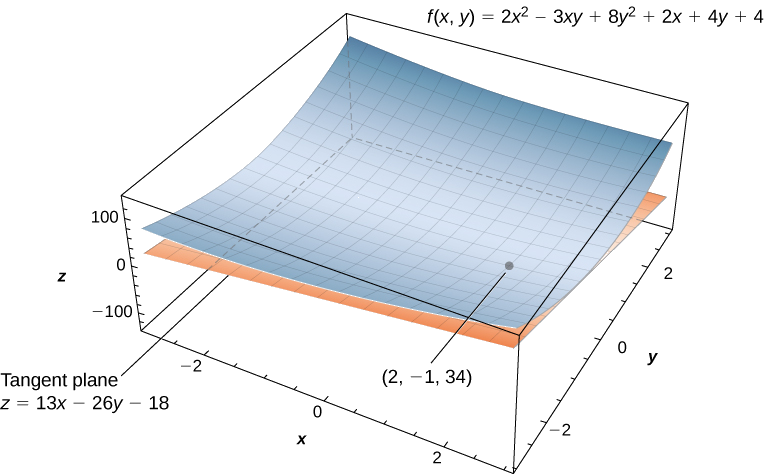



14 4 Tangent Planes And Linear Approximations Mathematics Libretexts
Click here👆to get an answer to your question ️ If 2x^2 3xy y^2 x 2y 8 = 0 then dydx =Consider y as a function of x defined implicitly by \begin{equation*} 2x^{2}y3xy^{2}=6 \end{equation*} The derivatives of both sides should be equal The derivative of the RHS is 0,Algebra Expressions, Equations, and Functions Expressions with One or More Variables



Www Ualberta Ca Csproat Homework Math 334 Assignment solutions Assignment 2 solutions Pdf




Assignment No
We think you wrote 2x^23xy2y^2/12x12y/x^2xy2y^2/x^2y^2 This deals with adding, subtracting and finding the least common multipleZ = x2y3 2x4y ∂z/∂x =2xy3 2 ∂z/∂y =3x2y2 4 • REMEMBER When you are taking a partial derivative you treat the other variables in the equation as constants!Equations Tiger shows you, step by step, how to Isolate x (Or y or z) in a formula 2x^2(dy/dx)=3xyy^2 and Solve Your Equation Tiger Algebra Solver When a product of two or more terms equals zero, then at least one of the terms must




Solutions To Implicit Differentiation Problems




Misc 4 Prove X2 Y2 C X2 Y2 2 Is General Solution Of
Solutions to exercises 15 Exercise 2 Standard form (y2 −2x)dx2xydy = 0 Exact if ∂P ∂y = ∂Q ∂x, where P(x,y) = y2 −2x Q(x,y) = 2xy ∂P ∂y = 2y = ∂Q ∂x ie ode is exact ∴ u(x,y) exists such that du = ∂u ∂x dx ∂u




Chapter 1 Partial Differential Equations Ppt Video Online Download




Partial Derivative Mcqs Assignement Maxima And Minima Rates



Http Cloudportal Sathyabama Ac In Coursematerial Staging Uploads Smta1105 Pdf




X 2 Y 2 3xy D Dx Dx 10y Dy Dx 2xy2 3y Pdf Free Download
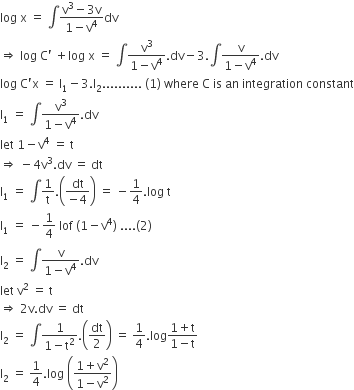



Prove That X2 Y2 C X2 Y2 2 Is The General Solution Of The Differential Equation X3 3xy2 Dx Y3 3x2y Dy Where C Is A Parameter From Class




Complex Differentiation Complex Number Analytic Function




Spiegel M R Schaum S Outline Of Vector Analysis Mgh 1968 Isbn x T 234s Docsity




Ex 5 3 6 Find Dy Dx In X3 X2y Xy2 Y3 81 Cbse



3 8 Implicit Differentiation Calculus Volume 1




Vector Analysis By Alimkanwalimtinaa Issuu



Q Tbn And9gct859ej0nhrohtfpzq7v Rju65qeexv33nwjgna9ul C2dc Vcw Usqp Cau



Http Web Mnstate Edu Jamesju Fall11 Content M323exam3f11prackey Pdf
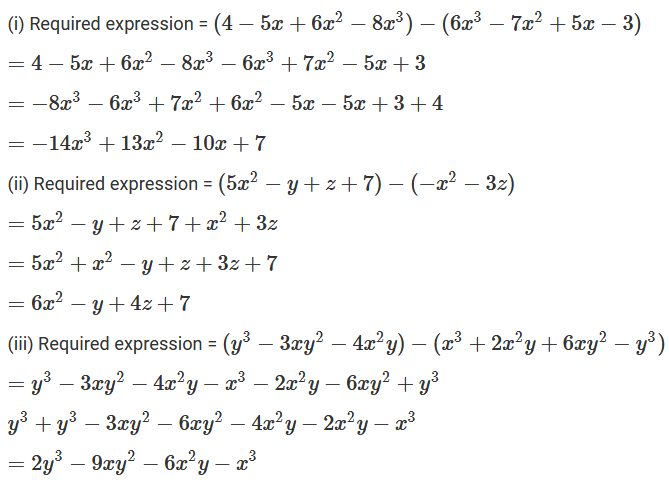



R D Sharma Solutions Class 7 Math Chapter 7 Algebraic Expressions Exercise 7 2




Ncert Exemplar Solutions For Class 7 Maths Chapter 10 Algebraic Expressions Available In Free Pdf Download




If X Y Are Integral Solutions Of 2x 2 3xy 2y 2 7 Then Value Of X Y Is



If X Y X Y X Y 3xy Then What Is X And Y Mathematics Solutions




X 3 3xy 2 Dx Y 3 3x 2y Dy Youtube




If X 2 And X Square Y Square 3xy 5 Then Find Y Brainly In




B Tech Ii Unit 4 Material Vector Differentiation




Pdf Complete Solutions Differential Equations With Modeling Applications Differential Equations With Boundary Value Problems 5th Edition Juan Carlos Becerra Linares Academia Edu



1



If W X Y Z X 2 Y 2 Z 2 X E T Y E T Sin T And Z E T Cos T Find Dw Dt Sarthaks Econnect Largest Online Education Community




Rd Sharma Solutions For Class 8 Chapter 6 Algebraic Expressions And Identities Download Free Pdf




1 Find And Sketch The Domain Of The Following Chegg Com




Systems Of Equations With Elimination 4x 2y 5 2x Y 2 5 Video Khan Academy



Http Www Math Sci Hokudai Ac Jp S Settepanella Teachingfile Calculus Calculus2 Pagine Lineintex Pdf




1 Find And Sketch The Domain Of The Following Chegg Com



Q Tbn And9gcqqdjererih8cbajqv Puntih4ikbw7iy9bdv7cgyhxgixkwubp Usqp Cau




15 3 Line Integrals Over Vector Fields Chapter 15 Vector Analysis Part Calculus Iii
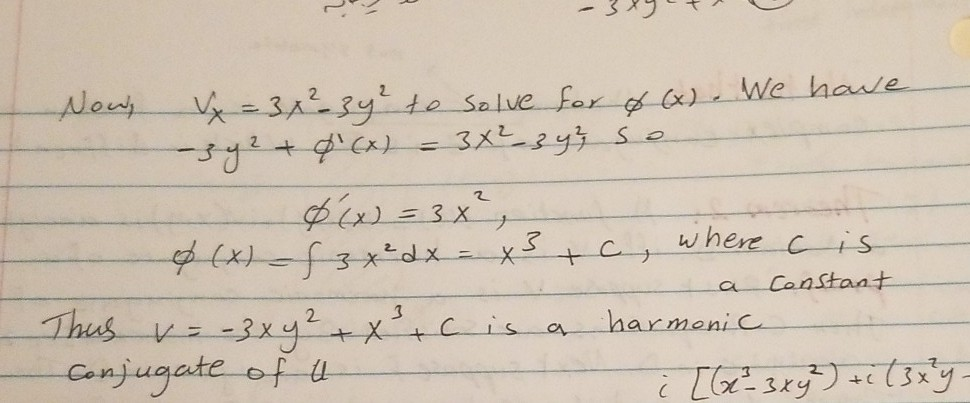



Exercises 1 Show That U X Y Is Harmonic In Some Chegg Com




Doc Partial Derivative Mcq S Assignement Innocentboy Nishant Academia Edu




Partial Differentiation




Pdf On The Diophantine Equation X2 Kxy Y2 2n 0




If X 3 Y 3 3xy 2 3x 2y 1 0 Then At 0 1 Dy Dx Youtube



Page 8 Algebraic High Resolution Stock Photography And Images Alamy




Differentiate X 2 Y 2 3xy 1 Youtube
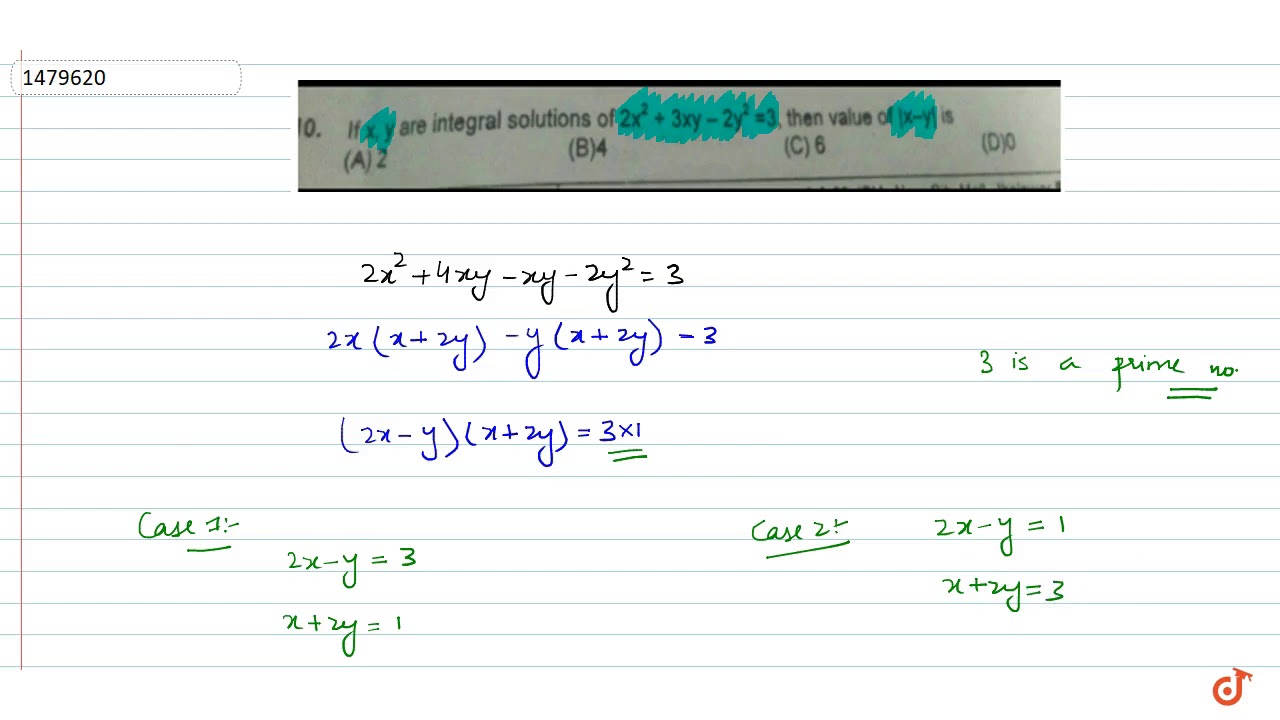



If X Y Are Integral Solutions Of 2x 2 3xy 2y 2 3 Then Value Of X Y Is Youtube



Web Maths Unsw Edu Au Cct Math19 Problems Answers Pdf




Exercises 1 Show That U X Y Is Harmonic In Some Chegg Com




Let F X Y 2x 2 3xy Y 2 X S T 2 And Y Chegg Com



Orion Math Iastate Edu Butler Calculus Exams Butler 265f11pt2asolns Pdf




If X 2 Y 2 3xy Then Choose The Correct Answer Of 2log X Y Form The Following Option




1 First Order Ordinary Differential Equations Pdf Free Download



If X 2 3xy Y 2 60 Where X And Y Are Real Determine The Maximum Possible Value Of Xy Quora



Http Hsrm Mathematik De Ws1617 Semester3 Komplexefunktionen Chapter3 Pdf




Btech Ii Engineering Mathematics Unit4
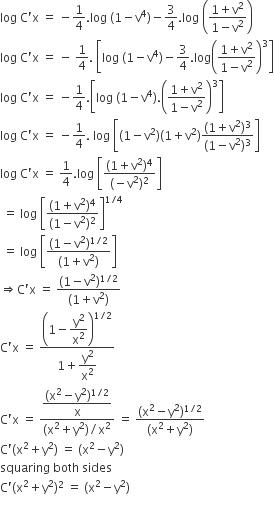



Prove That X2 Y2 C X2 Y2 2 Is The General Solution Of The Differential Equation X3 3xy2 Dx Y3 3x2y Dy Where C Is A Parameter From Class



Www Tau Ac Il Levant Ode Solution 6 Pdf



R D Sharma Solutions Class 7 Math Chapter 7 Algebraic Expressions Exercise 7 2



Prove That F X Y X 3 2x 2y 3xy 2 Y 3 Is Homogeneous What Is The Degree Verify Euler S Theorem For F Sarthaks Econnect Largest Online Education Community



If U X 2tan 1 Y X Y 2tan 1 X Y Prove That 2u Y X X 2 Y 2 X 2 Y 2 Sarthaks Econnect Largest Online Education Community



1




How To Find Y For Corresponding X Values Implicit Function Complex Number Stack Overflow




If U F R Where R 2 X 2 Y 2 Then 2u X 2 2u Y 2




Bear H S Understanding Calculus
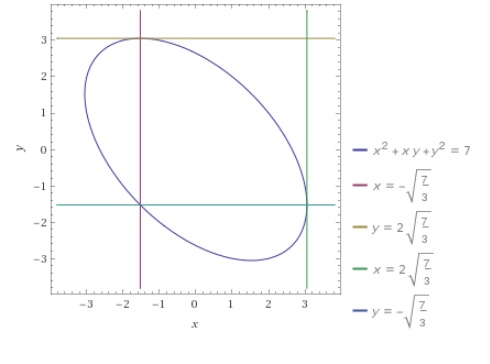



How Do You Find All Points On The Curve X 2 Xy Y 2 7 Where The Tangent Line Is Parallel To The X Axis And The Point Where The Tangent Line




Math 300 Problem Set 3 Solutions 1 Using The Cauchy Ubc Math




Prove That U X 2 Y 2 2xy 2x 3y Is Harmonic And Find Harmonic Conjugate V Edurev Iit Jam Question




Chapter 7 Calculus Of Several Variables




Maximize F X Y Xy Subject To X 2 Yx Y 2 1 Mathematics Stack Exchange




Show That The Equation Tex X 2 3xy 2 Y 2 2x 3y 35 0 Tex For Every Real Value Brainly In



Www Whitman Edu Mathematics Multivariable Multivariable 14 Partial Differentiation Pdf




If U Log X 2 Y 2 Z 2 Verify 2u X Y 2u X Y



Http Www2 Imperial Ac Uk Jdg Ae6soln Pdf




Differential Calculus Concepts Problems 126 Rd 1 Matrix



Answered If F X Y X 3xy 2x 3 Then F X H Y Bartleby




11 Business Math Stats Vol 2 Em Pages 51 100 Flip Pdf Download Fliphtml5




If The Equation Px 2 Y 2 Qz 2 2yz 2x 3xy 0 Represents A Pair Of Mutually Perpendicular Planes Then Q Is Equal To




1 First Order Ordinary Differential Equations Pdf Free Download




Find Dydx Where X 2 Y 2 3xy 1



Jntua Ac In Gate Online Classes Registration Downloads Material A Pdf




Solve The Differential Equation Y2 X2 Dy 3xy Dx 0 Maths Differential Equations Meritnation Com




Prove That X2 Y2 C X2 Y2 2 Is The General Solution Of The Differential Equation X3 3xy2 Dx Y3 3x2y Dy Where C Is Parameter Mathematics Shaalaa Com



If U X Y Z Xy 2z 3 X Sin T Y Cos T Z 1 E 2t Find Du Dt Sarthaks Econnect Largest Online Education Community




2 Partial Differentiation



Http Www Math Sci Hokudai Ac Jp S Settepanella Teachingfile Calculus Calculus2 Pagine Lineintex Pdf
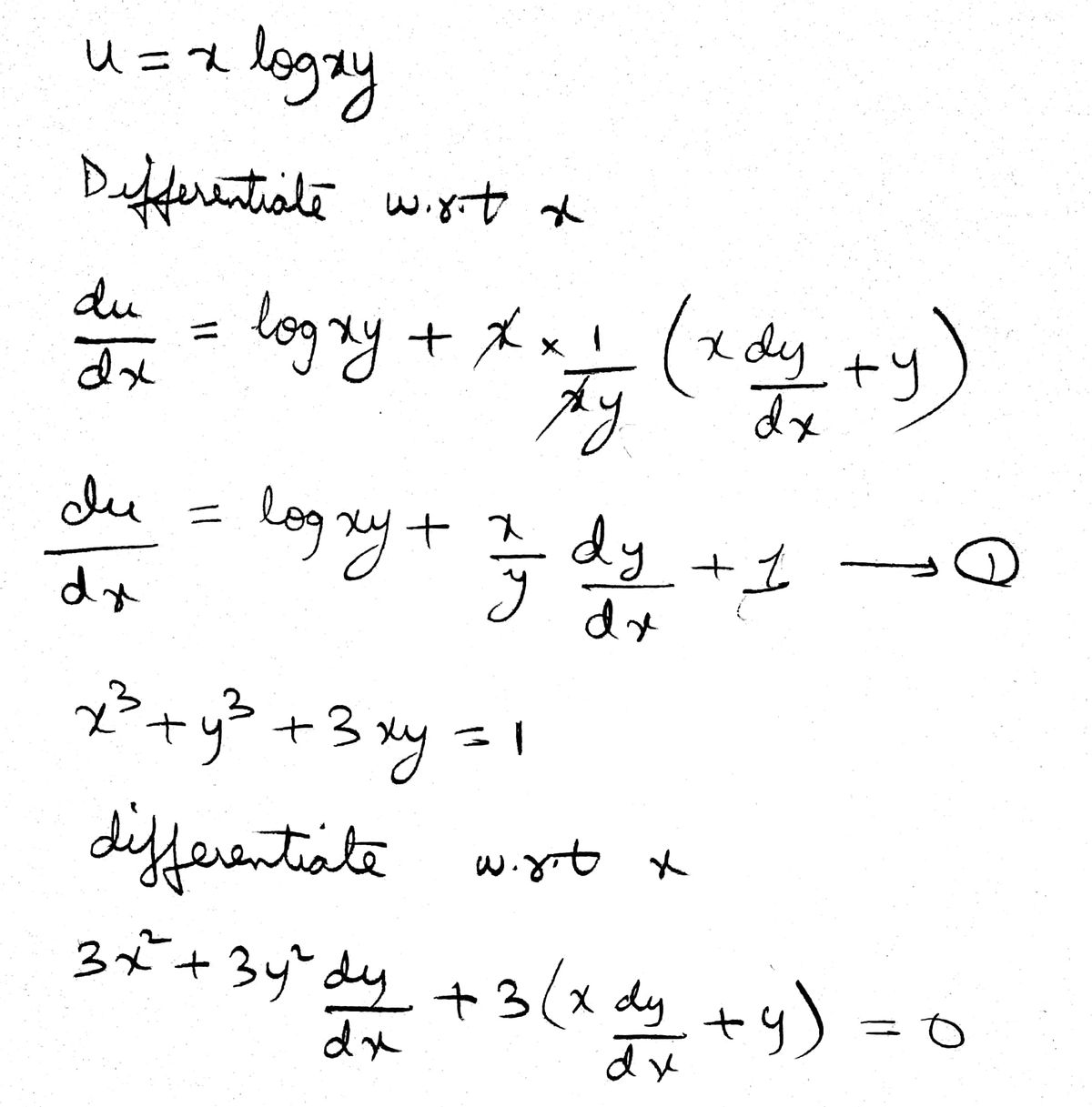



Answered If U X Log Xy Where X3 Y3 3xy 1 Find Bartleby




F X Y



0 件のコメント:
コメントを投稿