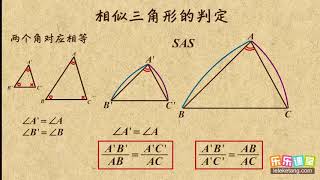
一、 教学目标 1 、掌握三角形相似的判定条件, 包括两角对应相等两三角形相似, 相似多边形的定义 会利用三角形相似的条件解决简单的问题 2 、经历探索两角对应相等两三角形相似的过程, 能进行有条理的思考并进行简单的推理证明 3 、经历自主探究、合作交流, 逐渐完善自己的想法, 感受到探索三角形相似的条件(1) 1、 小王师傅是数学玩具厂的质检员,他要对某种三角 形的文具进行检验(如图)。试问:他至少要测量多少 个数据,才能确认该文具合格(和模具一样)?说明你 的理由。 両方とも 数学の証明 のために必要なアイテムだから、テスト前には覚えなきゃいけないね。 念のためおさらいしておくと、 三角形の合同条件 3つの辺の長さがそれぞれ等しい 2組の辺の長さとその間の角が等しい 両端の角とその間の辺の長さがそれぞれ等しい 三角形の相似条件 3組の辺の比がすべて等しい 2組の辺の比とその間の角がそれぞれ等しい
相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス
直角三角形 相似条件
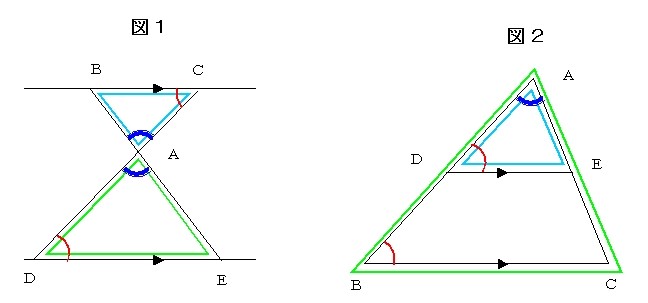
直角三角形 相似条件-直角三角形ABCと 青い直角三角形、緑の直角三角形はすべて相似になります。 直角三角形ABCと青い直角三角形は、角Bが共通、直角で、2角が等し く相似、同じように、直角三角形ABCと緑の直角三角形は、角Cが共通、 直角で、2角が等しく、この2つの三角形も相似になります。 直角三角形の合同条件には、以下の \(2\) つがあります。 条件①斜辺と 1 つの鋭角がそれぞれ等しい \(1\) つの角が \(90^\circ\) であることから、斜辺の長さおよび \(1\) つの鋭角が等しいことが示せれば、 残りの \(1\) 角も自ずと定まります 。




超级精品 初中数学几何模型
2、要同时满足六个元素,判定时感觉太繁,想不想找一些简单的方法来判定两个三角形相似呢? aas asa sas sss hl 只要确定三角形的形状,不必考虑其大小,究竟需要哪些条件呢? 运用三角形相似的定义进行合情推理。 四、应用拓展,达成目标 1.做一做,初步应用 判断题: (1) 有一个锐角对应相等的两个直角三角形相似。( ) (2) 所有的直角三角形都相似。( ) (3) 有一个角相等的两个等腰三角形相似。三角形 合同 相似条件 直角三角形の合同条件 中学数学 理科 寺子屋塾の復習サイト
O A B ^ B C O ^ A B C ^ = A B C ^ A B C ^ = 2 A B C ^ = 180 {\displaystyle {\widehat {OAB}} {\widehat {BCO}} {\widehat {ABC}}= {\widehat {ABC}} {\widehat {ABC}}=2 {\widehat {ABC}}=180} ° したがって A B C ^ = 90 {\displaystyle {\widehat {ABC}}=90} ° QED 芸術的な難問 良問数学 中2数学 複雑な多角形 角の和応用問題 今回は複雑な多角形の角の和の問題とその考え方です 星型など複雑な図形の角の和を求めるとき三角形の外角の定理やブーメラン型四角形の角リボン型ちょうちょ型の三角形の角の考え方が役立ちます直角三角形の合同条件 2つの直角三角形は、次の場合に合同である。 1 斜辺と1つの鋭角が、それぞれ等しいとき(証明) 2 斜辺と他の1辺が、それぞれ等しいとき(証明)
問2 下の図の三角形を、合同な三角形の組に分けなさい。また、そのとき使った合同条件をいいなさい。 3㎝ 3㎝ 3㎝ 3㎝ 5㎝ 5㎝ 5㎝ 5㎝ 5㎝ 5㎝ 70° ° ア イ ウ エ オ カ※ 特に,直角三角形では相似条件の③により 直角以外のもう一つの角が等しければ相似ということになります。 三角形相似的判定条件 两角对应相等,两个三角形相似;两边对应成比例且夹角相等,两个三角形相似;三边对应成比例,两个三角形相似;三边对应平行,两个三角形相似;斜边与直角边对应成比例,两个直角三角形相似;全等三角形相似。 1如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。 (简叙为:两角对应相等,两个三角形三角形の相似条件 とは、2つの三角形が相似であることを示すための条件です。 以下の3つの相似条件のうち、どれかが成り立つ場合、その三角形は相似であるといえます。 3組の辺の比がすべて等しい。 2組の辺の比が等しく、その間の角が等しい。




3 2 勾股定理的逆定理 Ppt Download




3 2 勾股定理的逆定理 Ppt Download
两个三角形相似的条件 文/张孟影 (1)平行于三角形一边的直线和其他两边和两边的延长线相交,所构成的三角形与原三角形相似; (2)如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似。動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru 多角形 相似条件 初等幾何学における多辺形(たへんけい、英 polylateral)または多角形(たかっけい、英 polygon;



1



28 2 解直角三角形及其应用 人教版九年级下册数学电子课本 数九网
三角形の相似条件は ① 3組の辺の日が等しい。 ② 2組の辺の比とその間の角が等しい。 ③ 2組の角が等しい。 探索三角形相似的条件 一、相似三角形 相似三角形:对应角相等,对应边成比例的两个三角形叫做相似三角形。 条件:(1)相似三角形的对应角相等 (2)相似三角形的对应边成比例 二、相似三角形的性质 对应性:两个三角形相似时通常把表示对应顶点的字母写在对应的位置上,这样写比较容易 三角形の相似条件 \(2\) つの三角形があり、それらが相似であるかどうかを判定する。 そのために、三角形の相似条件があります。 相似条件 \(3\) 組の辺の比がそれぞれ等しい \(2\) 組の辺の比とその間の角がそれ




超级精品 初中数学几何模型




相似三角形判定定理 相似三角形判定定理 數學公式 相似三角形的性質定理 百科知識中文網
三角形の相似条件、記号、相似比・面積比、証明問題 21年2月19日 この記事では、「相似」の意味や記号、三角形の相似条件、相似比と面積比について解説していきます。 また証明問題もわかりやすく説明していくので、ぜひマスターしてくださいね三角形相似条件、证明 一、判断三角形相似(与全等的对比) 相似三角形定义:三角分别相等,三边成比例的两个三角形 全等(特殊的相似) 相似 asa 两角对应相等的两个三角形相似 aas sas 两边对应成比例,且夹角相等的两个三角形相似 sss 对应边成比例的两个三角形相似 hl 直角三角形中,斜边与三角形の相似 次に直角三角形で考えてみましょう。 三角形の相似条件 2つの三角形が相似であることを調べるには、次の3つの方法を使い




中考數學滿分技法 相似三角形的存在探究問題 每日頭條




見圖拆圖 見到這些就和親爹一樣 角角相似一定手到擒來 每日頭條
三角形 相似条件 証明 三角形の相似条件とは、2つの三角形が相似であることを示すための条件です。 以下の3つの相似条件のうち、どれかが成り立つ場合、その三角形は相似であるといえます。 3組の辺の比がすべて等しい。两三角形相似的条件 作业帮 _____ 三种判别方法1有两个角对应相等;2两个边对应成比例,夹角相等;3三边对应成比例 证明图形相似的条件 _____ sss aaa sas aas ssa 平行于第三边的直线交另两条线的两三角形相似 性质中三角形全等是条件,结论是对应角、对应边相等(直角三角形は 竿の角度 だけで、「形」が決まりましたね!) 普通相似条件の「2組の角 がそれぞれ等しい」の1つは90°と決まってるし!でもよいですね (直角三角形は「斜辺中心主義」でしたね)
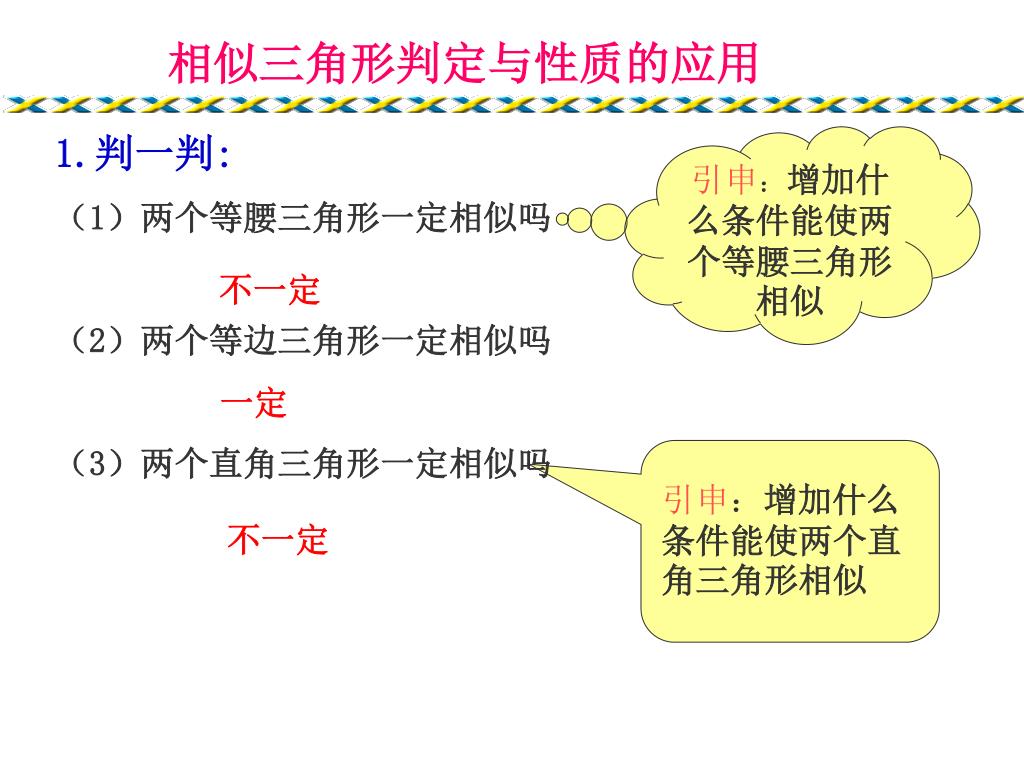



Ppt 相似三角形复习课powerpoint Presentation Free Download Id




初中数学相似三角形定理知识点总结 快资讯
三角形の相似条件 三角形の相似条件 2つの三角形は次の各場合に相似である。 1 3組の辺の比が、すべて等しいとき 2 2組の辺の比とその間の角が、それぞれ等しいとき




老师熬夜整理 初中数学最全几何模型大汇总 学生大呼 过瘾




老师熬夜整理 初中数学最全几何模型大汇总 学生大呼 过瘾




1000以上直角三角形相似条件 ニスヌーピー壁紙



这道初三几何题难倒不少人 解题关键是证明相似和构造直角三角形 文化资讯 娱乐新闻网
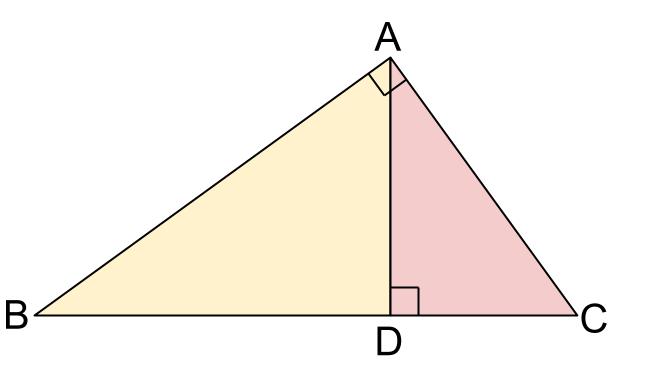



中学数学 直角三角形の相似 中学数学の無料オンライン学習サイトchu Su




中考数学丨压轴题攻略必备 相似三角形的6大模型总结 知乎




50 素晴らしい数学相似条件 最高のぬりえ




超级精品 初中数学几何模型
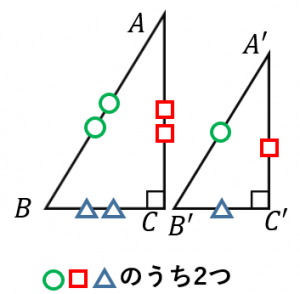



直角三角形の相似条件 具体例で学ぶ数学
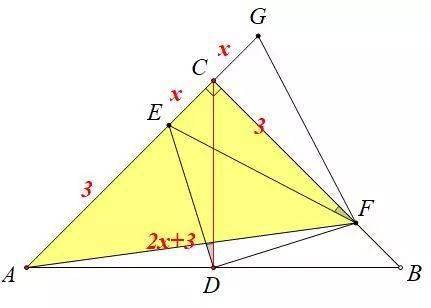



中考数学 等腰直角三角形 套路深 竟有这么多 基本图形 几何



1
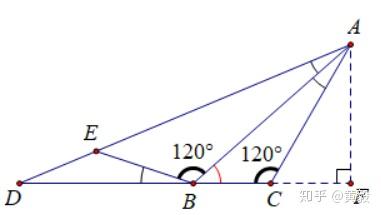



相似何其多 选准才能对 知乎




超级精品 初中数学几何模型
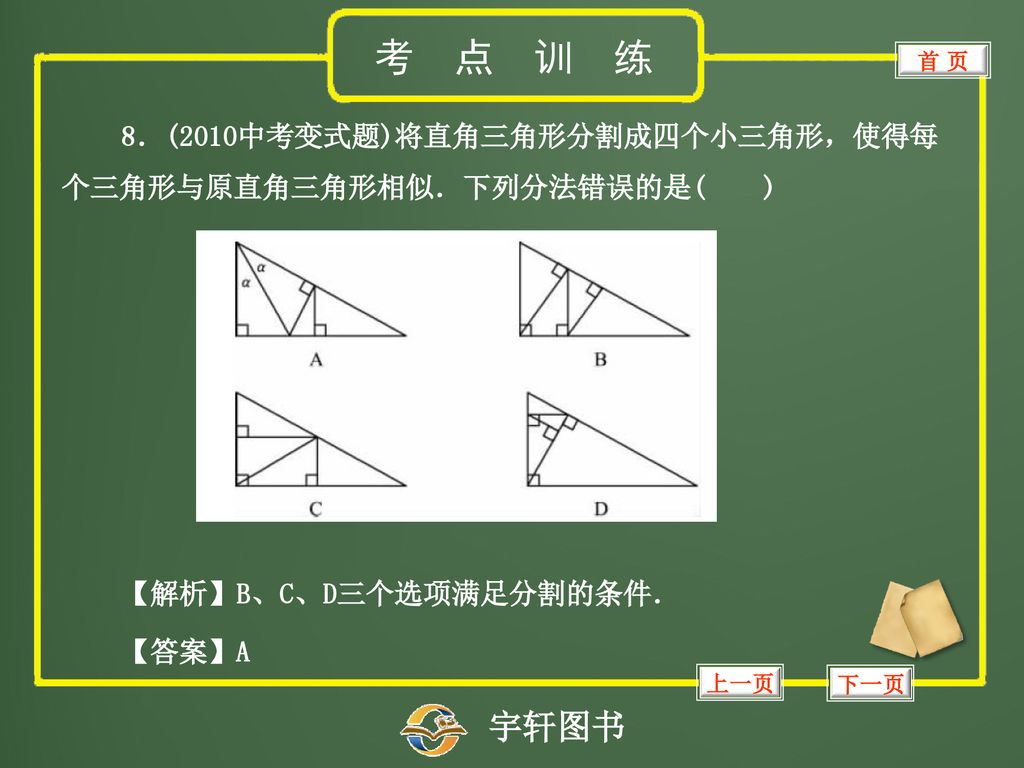



第19讲尺规作图与命题证明考点知识精讲中考典例精析举一反三考点训练 Ppt Download




直角三角形 维基百科 自由的百科全书




相似三角形知識學習歸類 學起來真輕鬆 每日頭條




相似三角形知識學習歸類 學起來真輕鬆 每日頭條
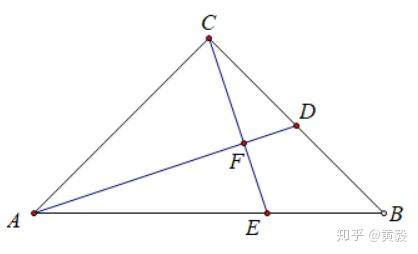



突破难点的关键是构造直角三角形相似基本型 知乎
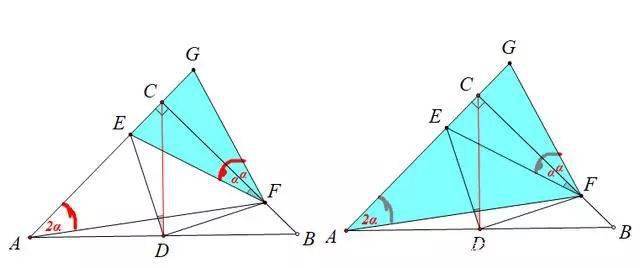



中考数学 等腰直角三角形 套路深 竟有这么多 基本图形 几何




三角形 相似與全等證明
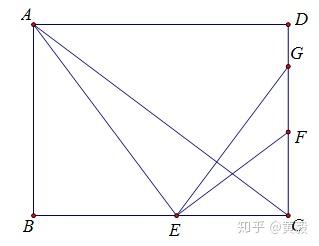



利用特殊直角三角形简化相似三角形存在性问题 知乎



三相似三角形的判定及性质 人教版高中选修4 1数学电子课本 数九网
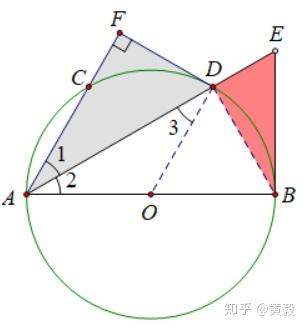



用方程思想求解圆内特殊角度 知乎




ぜいたく中3 数学相似 子供のための最高のぬりえ
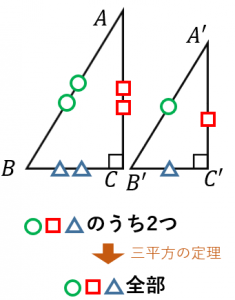



直角三角形の相似条件 具体例で学ぶ数学
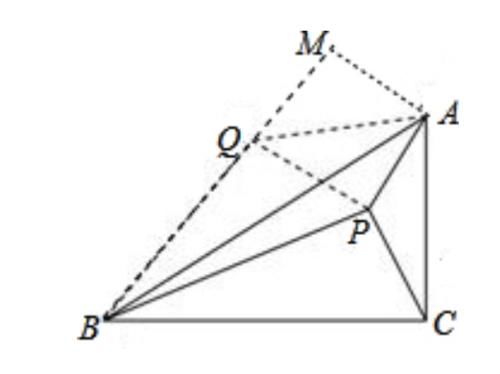



证明直角三角形相似的条件



1000以上直角三角形相似条件 ニスヌーピー壁紙




第24讲相似三角形考点知识精讲中考典例精析举一反三考点训练 Ppt Download




旋转背景下的面积比值问题 21年宜昌市中考数学第23题 三角形 直角 四边形 正方形 锐角 网易订阅



初三数学中一道求面积的题难倒众人 运用这个方法则可瞬间解决




利用特殊直角三角形简化相似三角形存在性问题 知乎



03相似三角形的判定图形的相似初中数学初三 Youtube



1000以上直角三角形相似条件 ニスヌーピー壁紙



中考数学专题复习 第18讲直角三角形 吉祥日历




見圖拆圖 見到這些就和親爹一樣 角角相似一定手到擒來 每日頭條




相似条件 合同条件 中学生 数学のノート Clear



1000以上直角三角形相似条件 ニスヌーピー壁紙
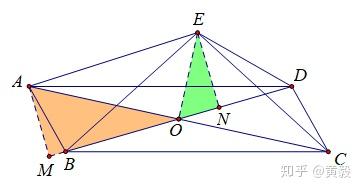



面积出发 相似搭桥 终成于双勾股 知乎



相似三角形应用举例 相似ppt课件 第一ppt



1000以上直角三角形相似条件 ニスヌーピー壁紙



受験数学かずスクール 三角形の合同条件と直角三角形の合同条件と三角形の相似条件




数学相似三角形知识点 相似三角形的性质和判定 星火网校



相似三角形应用举例 相似ppt 第1课时 第一ppt




初三相似三角形提高拓展专题练习附答案 豆知网



相似三角形应用举例 相似ppt课件 第一ppt
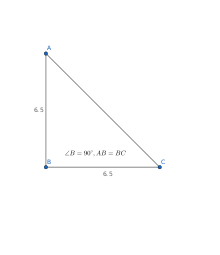



三角形 维基百科 自由的百科全书



相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス



1




保存版 三角形の合同条件と相似条件の6つのまとめ Qikeru 学びを楽しくわかりやすく
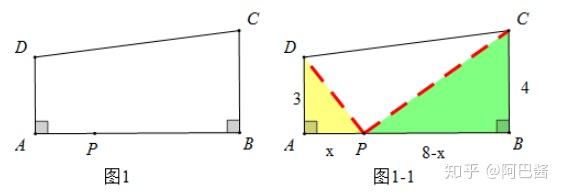



广猛说题系列之相似三角形存在性问题的通解通法 知乎



等腰直角三角形中的共斜边问题 一 方法



初中几何 相似三角形的判定 定理知识点归纳总结例题讲解基础练 初中数学 学习资料大全 免费学习资源下载
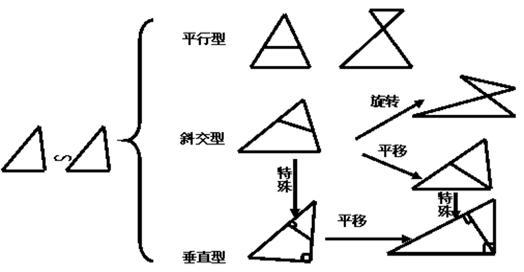



中考数学丨压轴题攻略必备 相似三角形的6大模型总结 知乎
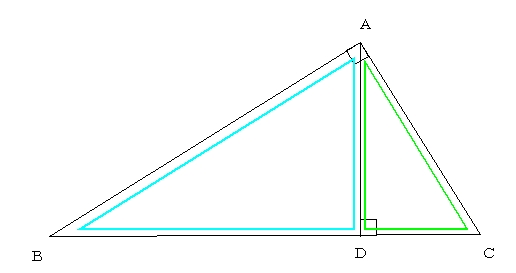



相似 直角三角形




27 2 3 相似三角形应用举例 初中电子课本网
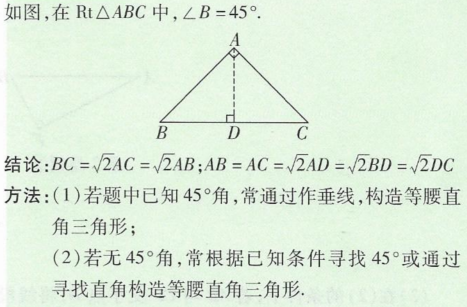



北京中考 四边形综合知识和思路 知乎



Studydoctor相似な三角形の辺の比 中3数学 Studydoctor




小升初几何没有难题 做完这几道先 2
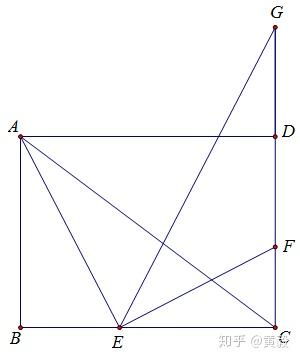



利用特殊直角三角形简化相似三角形存在性问题 知乎



1000以上直角三角形相似条件 ニスヌーピー壁紙



50 素晴らしい数学相似条件 最高のぬりえ



相似 直角三角形
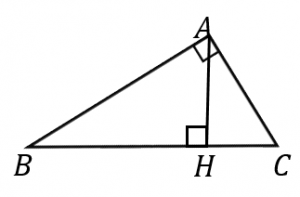



直角三角形の相似条件 具体例で学ぶ数学



中考数学专题复习 第18讲直角三角形 吉祥日历




1000以上直角三角形相似条件 ニスヌーピー壁紙
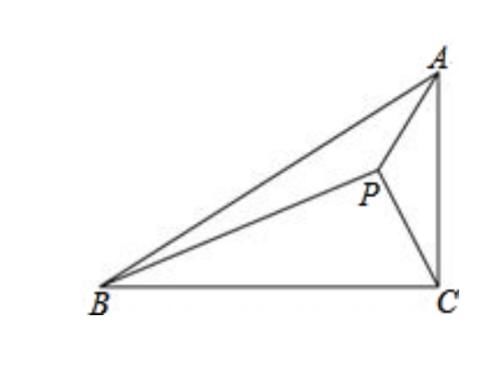



证明直角三角形相似的条件




九年级数学上册22 2相似三角形的判定第4课时相似三角形的判定定理3教案 沪科版 莲山课件




直角三角形之母子相似性質 Live 多媒體數學觀念典online




相似三角形的判定和判定方法归纳 星火网校



解直角三角形 锐角三角函数ppt课件3 第一ppt
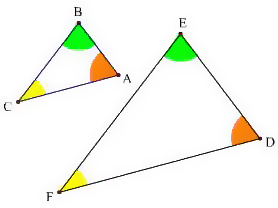



相似三角形 维基百科 自由的百科全书



相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス




全等三角形 维基百科 自由的百科全书
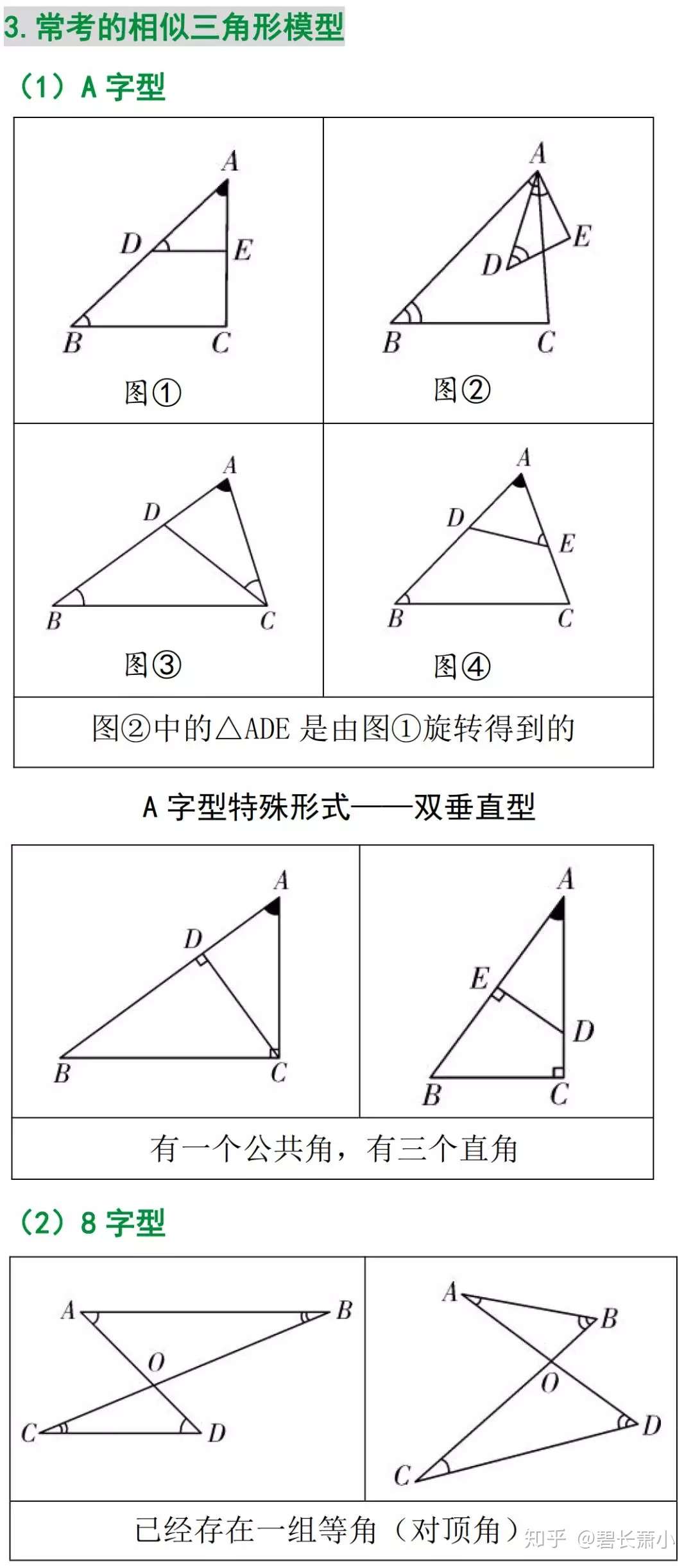



中考数学 相似三角形有关的证明与计算 知乎



1
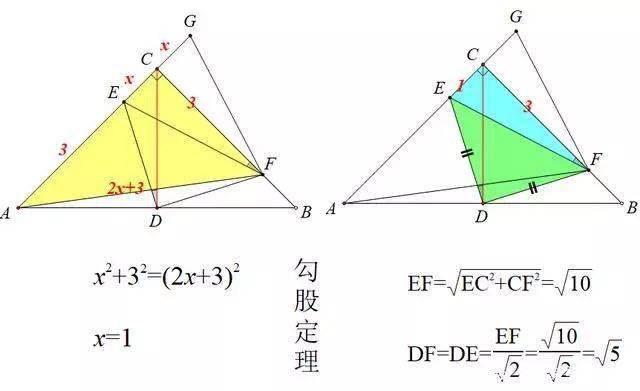



中考数学 等腰直角三角形 套路深 竟有这么多 基本图形 几何



直角三角形之母子相似性質 Live 多媒體數學觀念典online
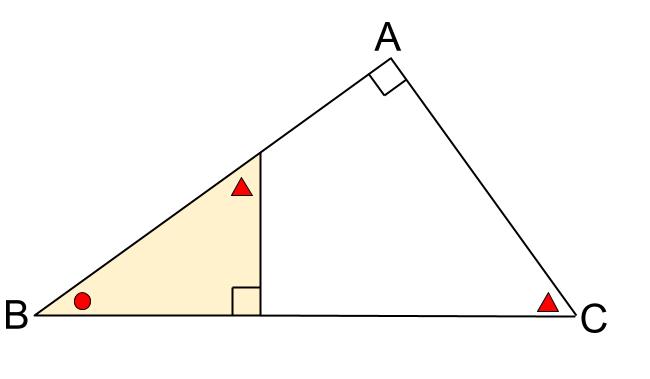



中学数学 直角三角形の相似 中学数学の無料オンライン学習サイトchu Su




50 素晴らしい数学相似条件 最高のぬりえ



三角形相似模型种 万图壁纸网
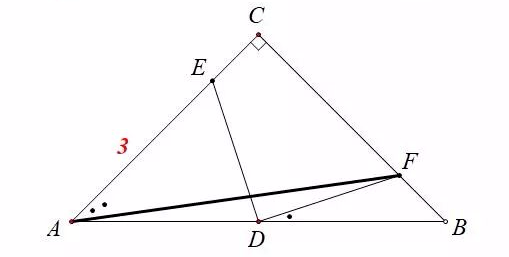



中考数学 等腰直角三角形 套路深 竟有这么多 基本图形 几何



探索相似三角形相似的条件 文档之家
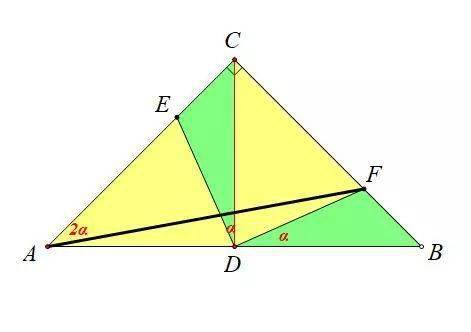



中考数学 等腰直角三角形 套路深 竟有这么多 基本图形 几何




50 素晴らしい数学相似条件 最高のぬりえ
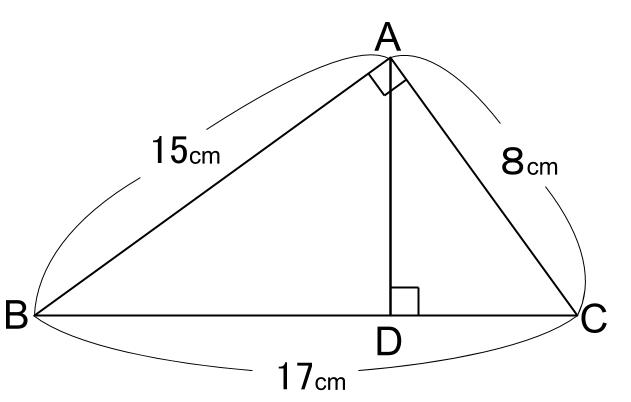



中学数学 直角三角形の相似 中学数学の無料オンライン学習サイトchu Su




中3数学 相似 直角三角形と相似 Youtube
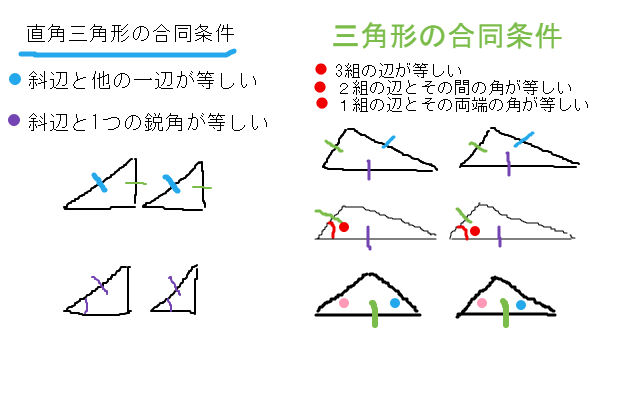



三角形 合同 相似条件 直角三角形の合同条件 中学数学 理科 寺子屋塾の復習サイト




探索三角形相似的条件 图形的相似ppt课件 Ppt课件下载 人人ppt




三角形の相似条件



学霸们 来看看这几道小升初后的入学分班数学压轴几何题 爱子网




老师熬夜整理 初中数学最全几何模型大汇总 学生大呼 过瘾




相似三角形判定定理 相似三角形判定定理 數學公式 相似三角形的性質定理 百科知識中文網




相似三角形定理和性质
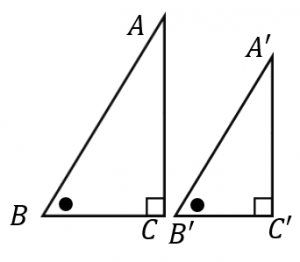



直角三角形の相似条件 具体例で学ぶ数学



0 件のコメント:
コメントを投稿