・連立2元1次方程式の必要性 と意味 ・連立2元1次方程式の解の意 味 2元1次方 程式,解, 連立方程 式,解く 1 (1) ② 連立方程式の 解き方 ・文字を消去することの意味 ・加減法による連立2元1次方 程式の解き方 ・代入法による連立2元1次方 程式の解き方連立3元1次方程式とは ・x+y=4 ・x−y=2 この2つの1次式を満たすxとyの値をもとめるには、連立方程式を解けばよかったですね。これまで学習してきた連立方程式は、基本的に文字が2つ、式が2つの組み合わせでした。 今回は、文字 なお、非同次の2元連立微分方程式を行列を用いて解くのは計算量がかなり多くなってしまうため、あまりおすすめできません。 (非同次の2元連立微分方程式であれば、2次の微分方程式にしてから解くのがおすすめです。) 6.練習問題 では、実際に

高校数学 2次方程式の実数解の個数 判別式 受験の月
2元1次方程式 解き方
2元1次方程式 解き方-復習連立方程式の解き方 連立方程式とは、一般的に \begin{eqnarray}\left\{\begin{array}{l}axby=c\\dxey=f\end{array}\right\end{eqnarray} といった形で表すことが多い式です。 2元1次方程式と呼ばれる「2つの変数(文字)」と「最大次数が1」の式で表方程式の解き方まとめ 方程式の基本的な解法手順は以下の通りです。 文字の項を左辺、数の項を右辺に移項する。 両辺をそれぞれ計算してまとめる。 x の前についている数が負の数の場合、両辺に×(-1)をして符号を変える。




中学2年生 数学 連立方程式の解き方 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
(1) 2元連立1次方程式の解と図形 次の例題を考えてみよう. 例題41 次の連立1次方程式を掃き出し法で解け. (a) 22 24 4 xy xy ìïï = í ïïî = (b) 22 24 0 xy xy ìïï = í ïïî = (a) の解説と解答 右の掃き出し表の S は例題31の ような'単位行列'にはできない第8章「1次方程式の復習」において2元1次連立方程式について,その解き 方を復習しました。この節ではそれを前提に連立の2次方程式の解き方を紹介し ます。 連立2次方程式の一般論はかなりの準備が必要となるのでここでは扱わず,後 で必要となる特別な(1元)1次方程式・・・・・1つの文字だけ(例えば x)の方程式 解く手順 (1)方程式の中にカッコがあれば、それをはずす (2)係数(単項式の数の部分)が分数や少数のときは、両辺に適当な数をか
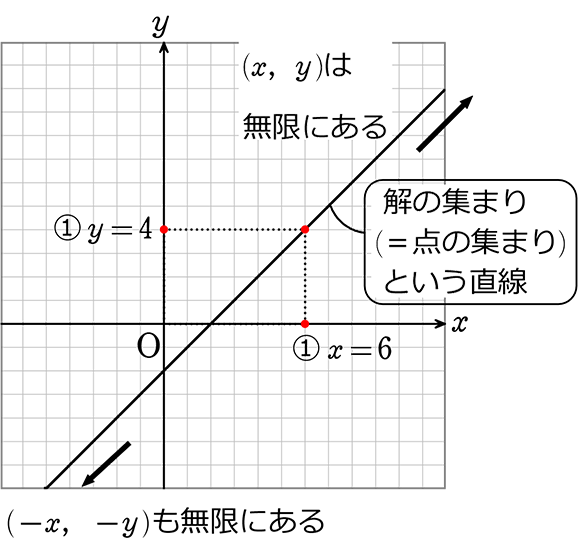
現在地 と前後の項目 2次方程式の解の公式を用いればどんな2次方程式でも解くことができますが,通常「簡単な方法でも解ける問題は,簡単な方法で解く」ようにし,複雑な方法は必要なときだけ使うようにします. (たとえ話:植木鉢をいじるには移植 2元1次方程式の解 2 2 元 1 1 次方程式の解は無限に存在します。 解とは何か、覚えていますか? 解とは、その方程式を成り立たせる値 のことです。 x2y = 9 x 2 y = 9 の解の1つは x = 1,y =4 x = 1, y = 4 です。 このように、 x x と y y の値の組が解になります。 先ほど解は無限に存在すると書きました。 確認しておきましょう。 例えば 2元1次不定方程式の解き方、2通り 数学 2x+3y=1(x、yは整数)① を解きましょう。 特に難しいというのでもなく、教科書にも載っている普通の問題です。 まず特殊解を見つけます。 つまり①を満たすx、yの具体例を見つけます。 カンで分かるでしょう。 x=ー1、y=1でよいですね。 するともちろん
連立方程式 複数の方程式が { でくくられたもの 全ての式をみたす値の組み合わせを 連立方程式の解 という 式が2つのものから100個のものまで連立方程式と呼びます。 ここでは2元1次方程式が2つあるものを扱っていきます。 例題をみてみましょう。2元1次方程式とは 2xy=8 のように 2つの文字を含む1次方程式が 2元1次方程式 で、 2元1次方程式を成り立たせる文字の値の組を 解 という。 2元1次方程式の解は無数にある。 例 2xy=8 の解は x=1,y=6 やx=2,y=4など 1 数学(2次方程式の)解の公式とは?覚え方、解き方、証明について、例題を計算しながら、わかりやすく解説しました2次方程式 中学数学 高校数学 11 (2次方程式の)解の公式とは;




連立3元1次方程式 身勝手な主張




連立方程式とその解 二元一次方程式とは何もの Qikeru 学びを楽しくわかりやすく
二元連立方程式 関数電卓が手元にないとき、面倒事を押し付けれて非常に助かります。 sqrt (値)のように使用します。 連立方程式の問題の答え合わせ。 とても便利でしたが途中の式や、分数表示ができない点が残念でした。 宿題の答え合わせに使いました。 途中式を表示していただけると分からなかった所を解きなおしできたりするのでお願いします。 使い 古代バビロニアの2次方程式の問題 まず、古代バビロニアの2次方程式に関する問題を見てみましょう。 "例えばスーサ出土の問題集(tms,no6)に, 「正方形の面積から,一辺の長さの4倍が引かれて780;問題21」 という問題があり(後略)" (引用元:中村 滋,室井 和男「数学史 If playback doesn't begin shortly, try restarting your device Videos you watch may be added to the TV's watch history and influence TV




中学2年生 数学 連立方程式の解き方 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




連立2元1次方程式を自由に解こう 中学2年生の数学 身勝手な主張
3元?連立方程式の解き方が分かりません。 Xのマイナス2乗の定積分 数学 16 極限の問題 数学 17 Mathematica で2元4次連立方程式を解くには・・・2元1次不定方程式特殊解の簡便法による求め方 ~互除法を用いたシミュレート (順行 )簡便法について 札幌旭丘高校 中村文則 ユークリッドの互除法は,最大公約数を求める高速アルゴリズムである.応用として簡便法を用い二元一次 a, b, c, d a,b,c,d a,b,c,d が整数の場合を考えます。 f ( x) = a x 3 b x 2 c x d f (x)=ax^3bx^2cxd f (x) = ax3 bx2 cxd とおきます。 f ( x 0) = 0 f (x_0)=0 f (x0 ) = 0 を満た




二次方程式の解の公式を使う問題で約分ができるパターンは難しい 中学や高校の数学の計算問題



不定方程式とは 問題の解き方を種類別にわかりやすく解説 受験辞典
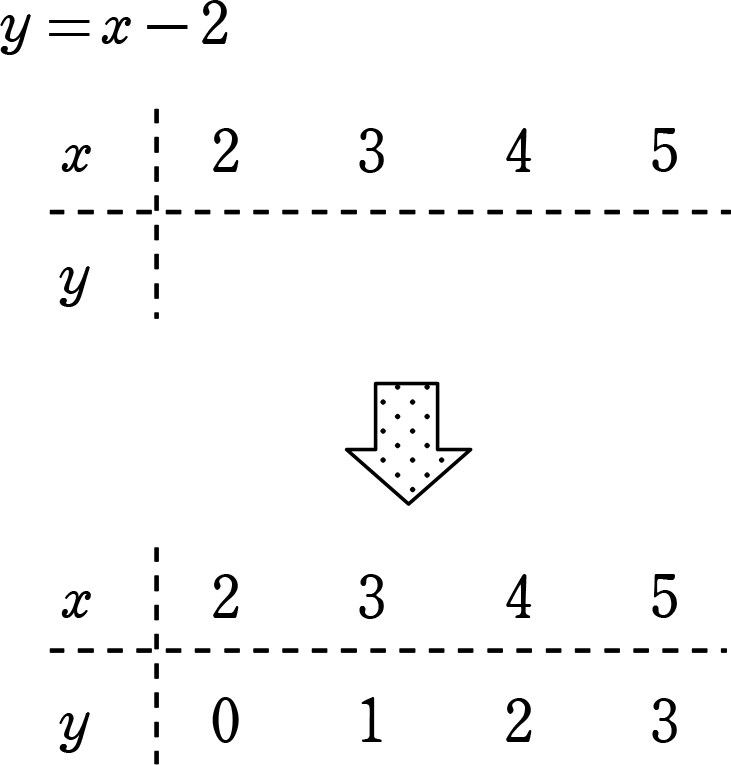
難しくはありません! 式が2つあるだけです (正確には、ここでは二元一次方程式が2つあるだけです) 先に軽くふれましたが、文字が2種類なら、等式が2つあれば、 解が1つに決まる というものですね。 では解き方です 《 例 》 次の連立方程式を解きそれでは,2 元1 次方程式の解と連立方程式の解について学習しましょう。 2 元1 次方程式2 x-3y=6 を成り立たせる ,yの値の組(x,y)を①~③の中からすべて 選びなさい。 ①(9,4 )②(1,5 )③(6,2 ここで行列の方程式の\(x\)は\(x_1\)と\(x_2\)の列ベクトルを表しています。 ではこの手順に従って連立方程式を解いてみましょう! まずは連立方程式を行列の形に変形します。 \ $$\left\left = \left$$ 次は逆行列を求めていくよ 逆行列の求め方は覚えていますか?



1次方程式と2元連立1次方程式



連立一次方程式 を高速に効率よく解くために 計算基礎科学連携拠点
今回は、補足として2元2次連立方程式の解き方を見ていこう。 基本的な考えは、連立方程式と同じで、文字を減らすことを考えればよい。 前回 ←2次方程式の解き方(3)(難) 次回 →解の問題(1)(代入、解から式を作る、直前の形)(基~標)次の式があるとします。 x 2y 3z = 2x 5y 9z = 100 5x 7y 8z = 0 これらの方程式をx 、 y 、 zについてどのように解くべきですか?可能であれば、Rやその他のコンピュータツールを使って、これらの方程式を解きたいと思います。学習日 年 月 日 1 解の公式を使って、二次方程式 2 x x 3 5 1 0 を解きなさい。 2 次の二次方程式を解きなさい。 ⑴ x2 3 9 ⑵ ⑶ 2 x x 10 24 0 ⑷ 2 x x 2 3 3 ある数 を2乗し、それを3倍すると9になりま



Iseqi Pukiwiki




一次不定方程式 当てはまる整数解 特殊解 の求め方 すうがくブログ 式変形ch
抵抗に関する連立方程式を解く必要がある。そこで,「キルヒホッフの法則」を説明する前に,ここ では数学的な準備として,未知数が二つの2 元連立1 次方程式と変数が三つの3 元連立1 次方程式に ついて,クラーメルの公式による解法を説明する。 12次方程式の解の公式 2次方程式をax 2 bxc=0の形にして、公式に当てはめれば全ての2次方程式は解くことができる。 中1数学にでてくる1次方程式(xの方程式)の解き方 こんにちは!イボコロリを使ってみたKenだよ。 中1数学でむずかしいと言われているのは「方程式」。中1で勉強するのは「 1次方程式 」とよばれているものだ。なにせ、文字が1つしか含まれていないから



第1章 連立方程式




中2 二元一次方程式 解の求め方 日本語版 Youtube
2元1次方程式(axby=p,cxby=qの法則) 作者 S9nine さん 実行数 923 2元1次方程式(axby=p,cxby=qの法則) 作者 31 2次方程式の解き方 311 基本的な2次方程式の解き方(1)(基) 312 2次方程式のの解き方(2)(展開・置き換え・二乗利用)(標) 313 2次方程式の解き方(3)(たすき掛け、係数が平方根、文字係数)(難) 314 補題・2元2次連立方程式 32子供向けぬりえ ロイヤリティフリー3 元 2 次 連立 方程式 解き方 2元1次方程式 無料で使える中学学習プリント 連立方程式で3つの式がある時の解き方が誰でも分かる 高校生向け受験応援メディア 受験のミカタ 高校数学a 2元1次不定方程式 Ax By C の整数解



二次方程式の解の公式 因数分解による解き方を解説 解の公式をマスター Studyplus スタディプラス
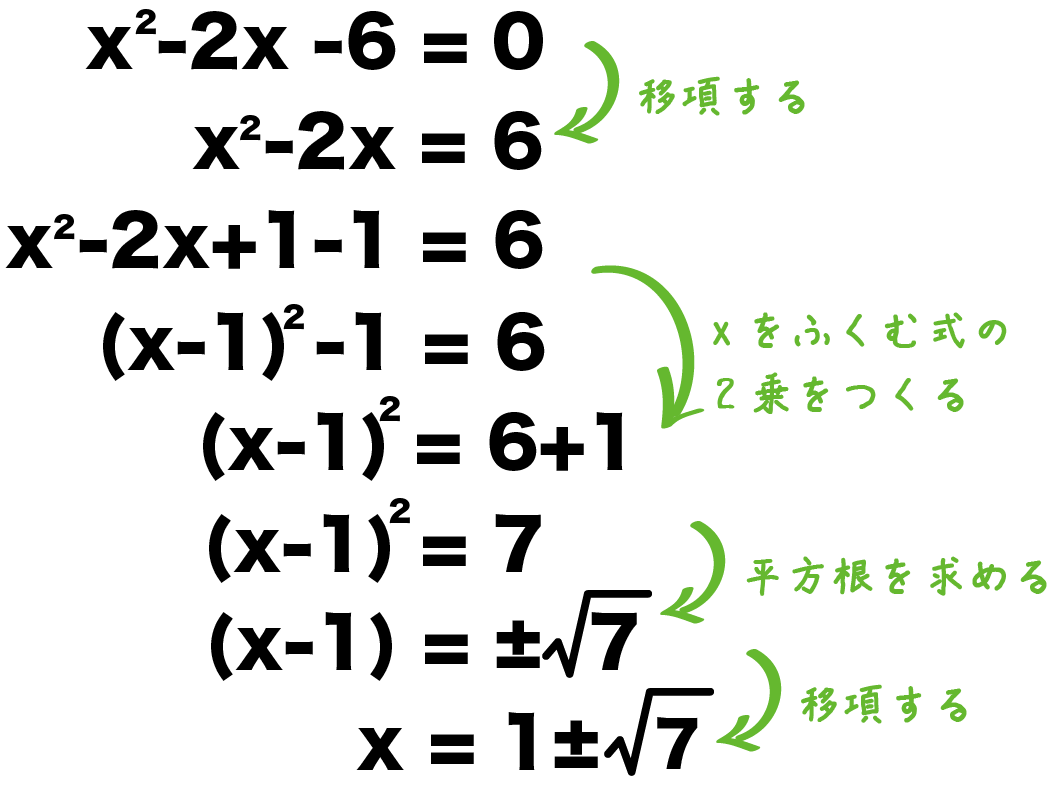



中3数学 二次方程式の解き方を見分ける1つのコツ Qikeru 学びを楽しくわかりやすく
目次 1 1次不定方程式の単元で学習すること 2 1次不定方程式について 3 1次不定方程式の解き方と解の表し方 31 1次不定方程式の解き方 32 1次不定方程式の一般解を求めてみよう 4 1次不定方程式を扱った問題を解いてみよう 41 問(1)の解答・解説;4元1次方程式 { a 11 x 1 a 12 x 2 a 13 x 3 a 14 x 4 = b 1 a 21 x 1 a 22 x 2 a 23 x 3 a 24 x 4 = b 2 a 31 x 1 a 32 x 2 a 33 x 3 a 34 x 4 = b 3 a 41 x 1 a 42 x 2 a 43 x 3 a 44 x 4 = b 4
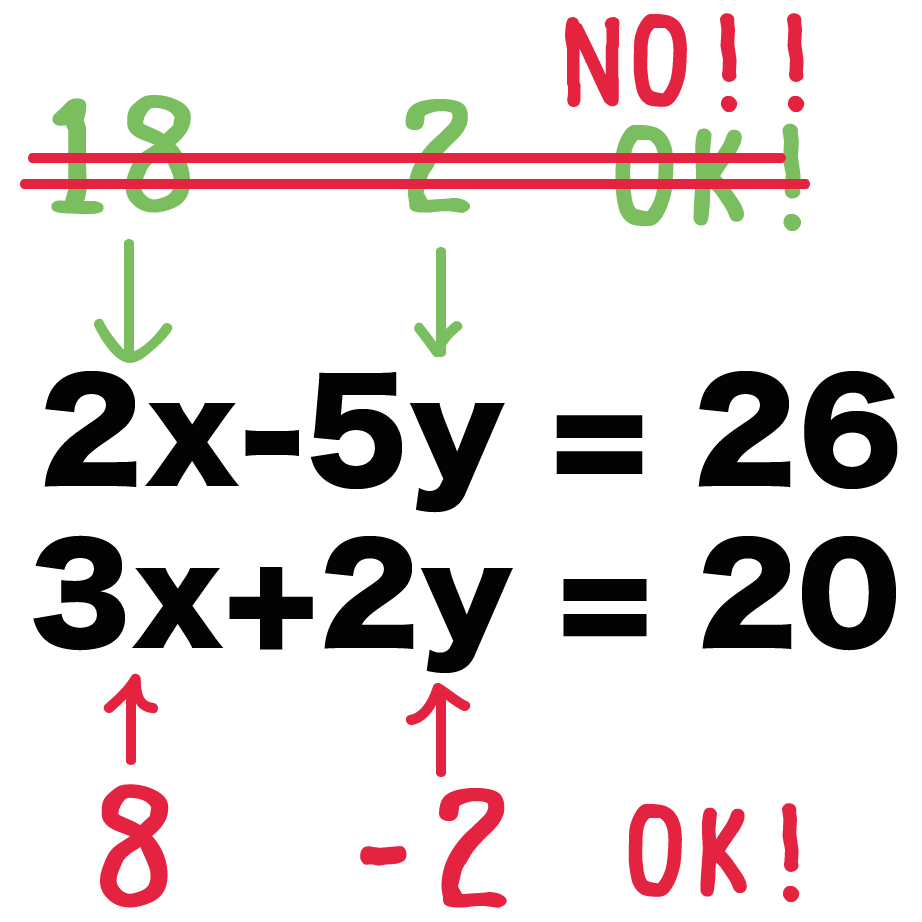



連立方程式とその解 二元一次方程式とは何もの Qikeru 学びを楽しくわかりやすく




Libreoffice で3 元1 次方程式を解く話 Sawakaze Blog




高校数学 2次方程式の実数解の個数 判別式 受験の月




第4回講義 基礎数学



Q Tbn And9gcsc Kue4fyxt0rbsfn6hdi7bdwdccy Iyksoshpenrntx 0cwmu Usqp Cau




連立方程式とその解 二元一次方程式とは何もの Qikeru 学びを楽しくわかりやすく



第1章 連立方程式




第4回講義 基礎数学 数学入門



第1章 連立方程式




連立方程式で3つの式のある3元1次方程式とは 3元連立方程式の解き方をわかりやすく解説 Himokuri
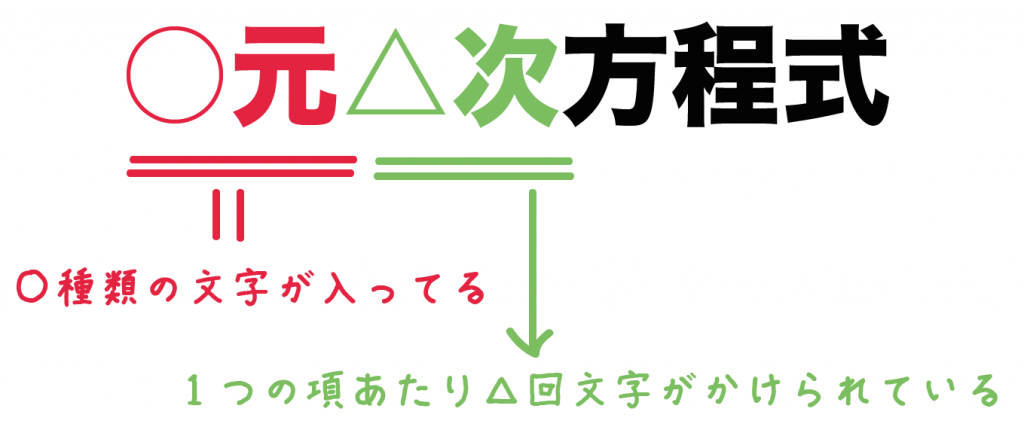



連立方程式とその解 二元一次方程式とは何もの Qikeru 学びを楽しくわかりやすく
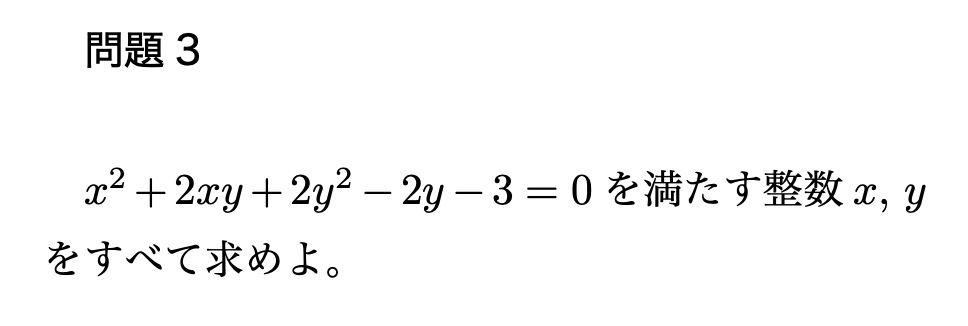



不定方程式の解き方とは 全4パターンを東大医学部生がわかりやすく解説 東大医学部生の相談室
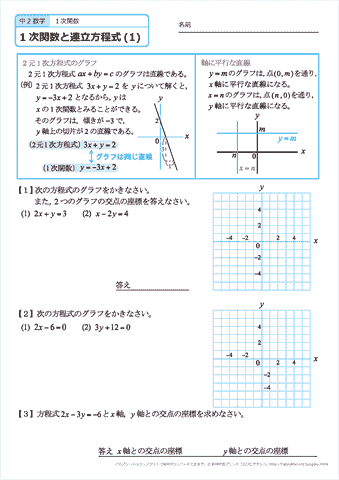



中学2年生 数学 1次関数と連立方程式 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中2数学 二元一次方程式 証明 中学生 数学のノート Clear




高校数学 3元連立1次方程式 一般型と循環型 受験の月



3




食塩水の濃度に関する連立2元1次方程式の応用問題 中学校2年生の数学より 身勝手な主張



Http Kore Mitene Or Jp Tohru Eq 00 Pdf



Rで連立一次方程式の解を求める Arupaka Arupakaの日記



Http Www Juen Ac Jp G Katei Nunokawa Function 2 2 5 Pdf




高校数学 2元2次連立方程式3パターン 受験の月




3分で分かる 式が3つの連立方程式の解き方をわかりやすく解説 合格サプリ




連立方程式とその解 二元一次方程式とは何もの Qikeru 学びを楽しくわかりやすく




トップ100 方程式 の 利用 解き方 最高のぬりえ




数学 中2 35 二元一次方程式のグラフを書く Youtube
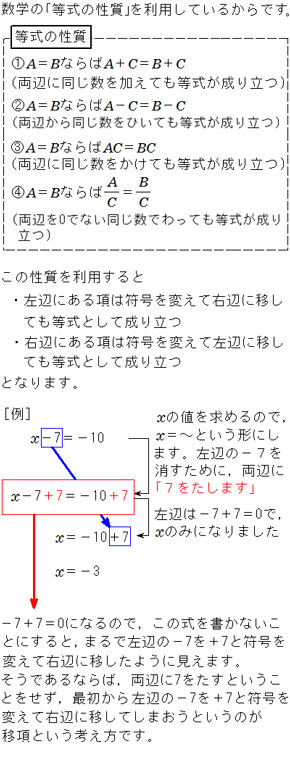



1次方程式 なぜ移項するとき符号がかわるのか 中学生からの質問 数学 進研ゼミ中学講座 中ゼミ



数学で2元1次方程式を習いますが そもそも元というのはどう言う意味でしょう Yahoo 知恵袋




食塩水の濃度に関する連立2元1次方程式の応用問題 中学校2年生の数学より 身勝手な主張




連立方程式とその解 まなびの学園




連立2元1次方程式を自由に解こう 中学2年生の数学 身勝手な主張



第1章 連立方程式




この問題の解き方を教えてください お願いします Clear




要点 連立3元1次方程式の解き方 Youtube
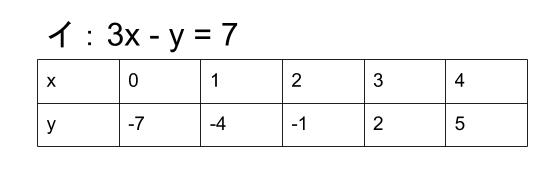



中学数学 2元1次方程式と連立方程式 中学数学の無料オンライン学習サイトchu Su




行列式 方程式の解 Cramerの公式 余因数展開 Ppt Download




2次関数26 連立3元1次方程式 怜悧玲瓏 高校数学を天空から俯瞰する




二元一次方程式にする前の掛け算はなぜこのようなかけ方法を行ってるのですか Clear
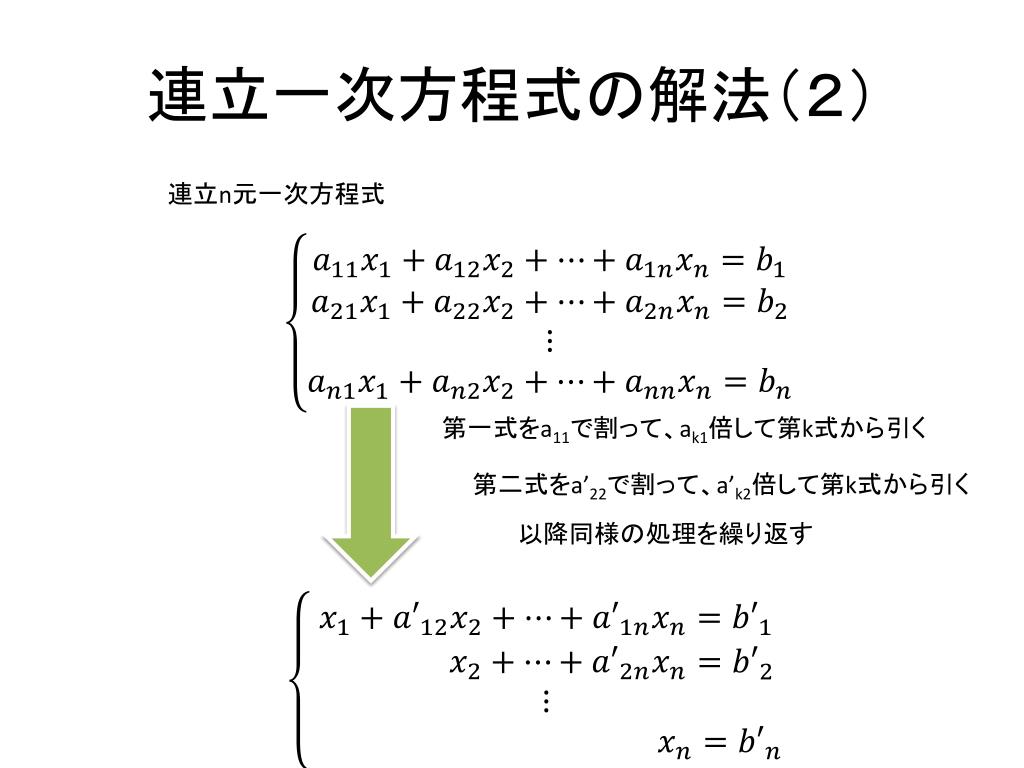



Ppt 連立一次方程式の解法 1 Powerpoint Presentation Free Download Id




高校数学 2式が互いに対称な連立方程式 和と差で組み直せ 受験の月




Xyz 3つの式の連立方程式の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




連立方程式 連立方程式の意味と一般的な解法



中学数学 連立方程式 二元一次




この三元一次方程式の解き方を教えて下さい Clear



中3 二次方程式の解き方 平方根 因数分解 中学数学の方程式 中間 期末テスト 高校入試対策
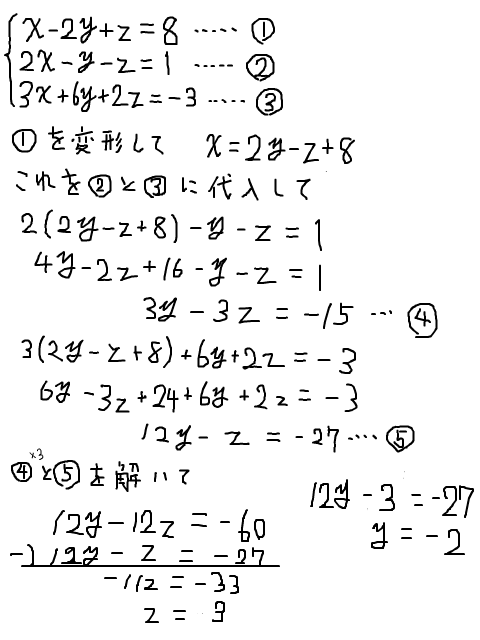



きゃおす 連立3元1次方程式 解いてみた 手書きブログ
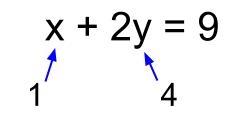



中学数学 2元1次方程式と連立方程式 中学数学の無料オンライン学習サイトchu Su




連立方程式の解き方とは 代入法か加減法で計算しよう 分数の問題や文章題アリ 遊ぶ数学



2次方程式の解き方 補足 二元二次連立方程式 難 数学の解説と練習問題




不定方程式ax by c c 0 の整数解の求め方 数学 苦手解決q A 進研ゼミ高校講座




連立方程式で3つの式がある時の解き方が誰でも分かる 高校生向け受験応援メディア 受験のミカタ



二次方程式の意味と解き方まとめ 解の公式 因数分解 アタリマエ



Gakuto Co Jp Docs Download Pdf H28 Sugaku2 Seitoyoutest 2 1katiou Pdf



中3 二次方程式の文章題 中学数学の方程式 中間 期末テスト 高校入試対策




1次方程式 小数 分数をふくむ1次方程式の解き方 中学数学 定期テスト対策サイト




連立3元一次方程式でこのように詰んでしまいます Clear




連立二元一次方程式をいろいろな方法で解いてみよう 身勝手な主張



中学数学 連立方程式 二元一次




整数16 一次不定方程式が5秒で解けるとか無理じゃね 怜悧玲瓏 高校数学を天空から俯瞰する



第1章 連立方程式




連立3元1次方程式 身勝手な主張




高校数学 文字係数の2元連立1次方程式 受験の月
(%E3%80%80)%E2%97%8F.png)



中学数学 二次方程式




1次関数と2元1次方程式の違い Youtube




2次関数26 連立3元1次方程式 怜悧玲瓏 高校数学を天空から俯瞰する




高校数学 文字係数の1次方程式 受験の月




2次関数26 連立3元1次方程式 怜悧玲瓏 高校数学を天空から俯瞰する




โน ตของ 数学 中ニ 3元1次方程式の計算 ช น Junior Clear




中2数学 連立方程式 1 1 2元1次方程式 Youtube
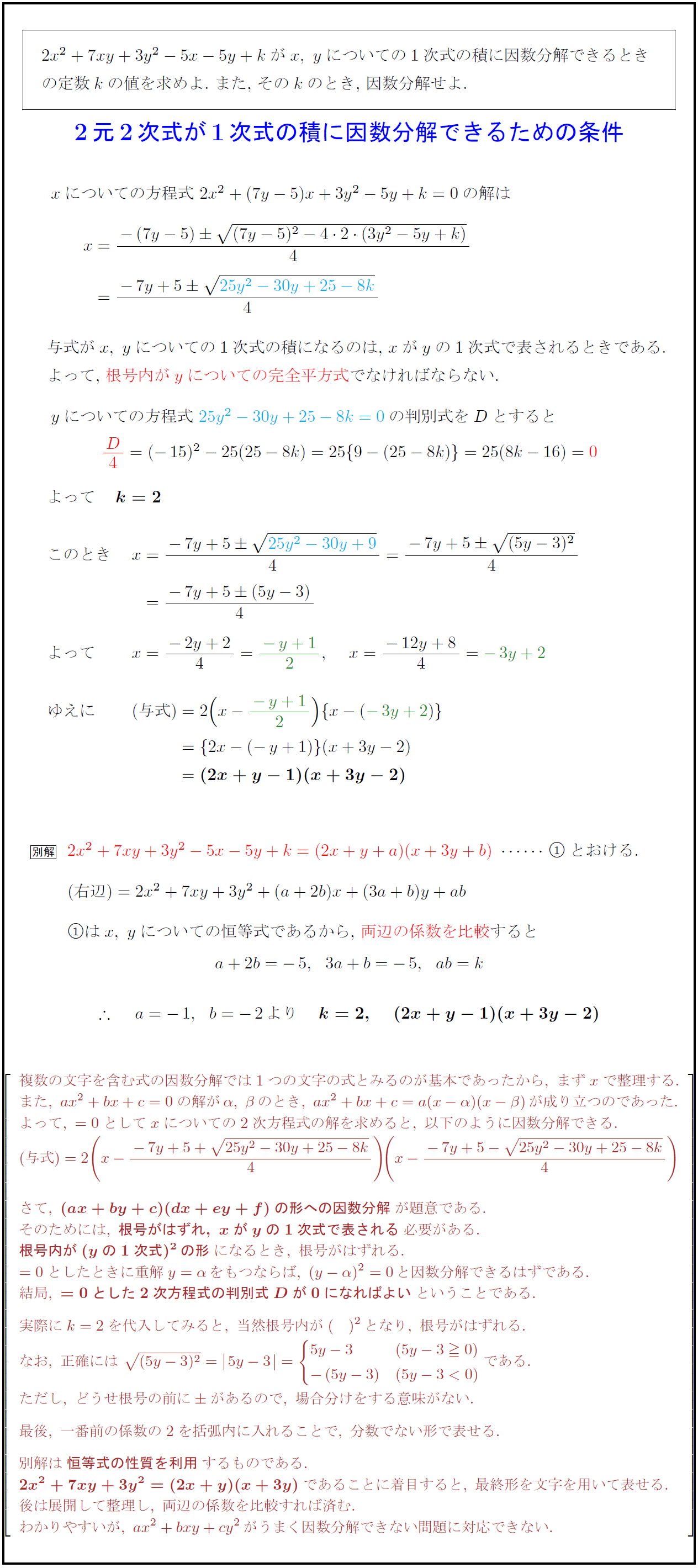



高校数学 2元2次式が1次式の積に因数分解できるための条件 受験の月




2元1次方程式 無料で使える中学学習プリント



Q Tbn And9gcqoppv54w Mvafcpiij8jce2rg7skwmo35us2er Uud Uzjtbx Usqp Cau




二元一次方程解法



連立一次方程式 を高速に効率よく解くために 計算基礎科学連携拠点



Studydoctor2元1次方程式とグラフの書き方 中2数学 Studydoctor




中学数学 中学2年 Vol 017 連立方程式の解き方 連立方程式とその解 二元一次方程式 Youtube



1




連立方程式とその解 二元一次方程式とは何もの Qikeru 学びを楽しくわかりやすく




3分で分かる 一次方程式の解き方と検算方法 練習問題つき をわかりやすく 合格サプリ



連立方程式とその解 二元一次方程式とは何もの Qikeru 学びを楽しくわかりやすく



48s96ub7b0z5f Net Gojoho Futeihouteishiki




5 連立一次方程式 Ppt Video Online Download




二元一次方程式の文章題のやり方とこの写真の問題と 解き方を教えて欲しいです Clear




連立3元1次方程式 まなびの学園




二次方程式の解き方をわかりやすく解説 高校生向け受験応援メディア 受験のミカタ
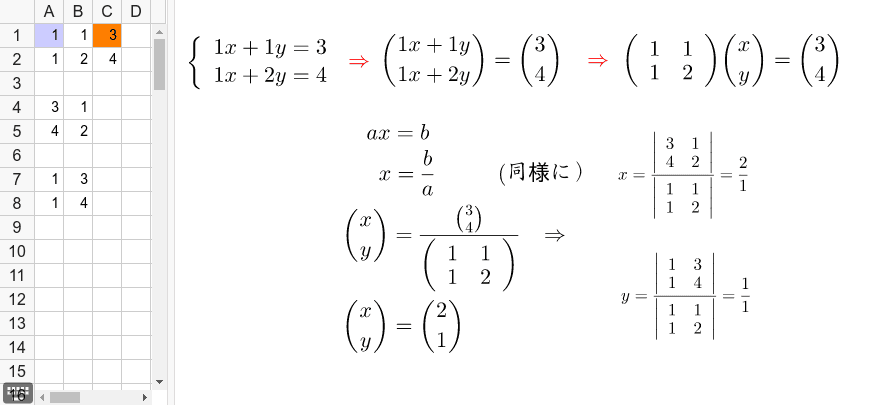



二元一次連立方程式 Geogebra




2つの解法 2元2次方程式の整数解 双曲線形 数学a 整数 Youtube




一次方程式の解の求め方 数学fun




二次方程式の解がわかっている問題は xに代入して計算しよう 中学や高校の数学の計算問題




例題 連立3元1次方程式の解き方 Youtube




二次方程式とは 見分け方が簡単にわかる中学レベルの問題 中学や高校の数学の計算問題



0 件のコメント:
コメントを投稿